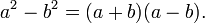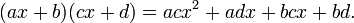Binomial
From Wikipedia, the free encyclopedia
Not to be confused with Binomial distribution.
For other uses, see Binomial (disambiguation).
In algebra, a binomial is a polynomial with two terms[1] —the sum of two monomials—often bound by parentheses or brackets when operated upon. It is the simplest kind of polynomial after the monomials.
Operations on simple binomials
- The binomial
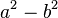 can be factored as the product of two other binomials.
can be factored as the product of two other binomials.
- This is a special case of the more general formula:
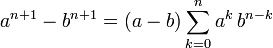 .
. - This can also be extended to
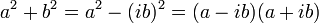 when working over the complex numbers
when working over the complex numbers
- The product of a pair of linear binomials
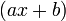 and
and 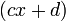 is:
is:
- A binomial raised to the nth power, represented as
- can be expanded by means of the binomial theorem or, equivalently, using Pascal's triangle. Taking a simple example, the perfect square binomial
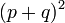 can be found by squaring the first term, adding twice the product of the first and second terms and finally adding the square of the second term, to give
can be found by squaring the first term, adding twice the product of the first and second terms and finally adding the square of the second term, to give  .
.
- A simple but interesting application of the cited binomial formula is the "(m,n)-formula" for generating Pythagorean triples: for m < n, let
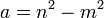 ,
, 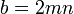 ,
, 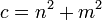 , then
, then  .
.
See also
- Binomial theorem
- Completing the square
- Binomial distribution
- Binomial coefficient
- Binomial-QMF (Daubechies Wavelet Filters)
- The list of factorial and binomial topics contains a large number of related links.
- Binomial series
Notes
- ↑ Weisstein, Eric. "Binomial". Wolfram MathWorld. Retrieved 29 March 2011.
References
- L. Bostock, and S. Chandler (1978). Pure Mathematics 1. ISBN 0-85950-092-6. pp. 36
- Hazewinkel, Michiel, ed. (2001), "Binomial", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.