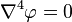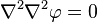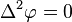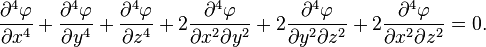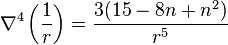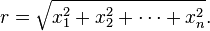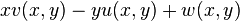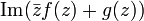Biharmonic equation
In mathematics, the biharmonic equation is a fourth-order partial differential equation which arises in areas of continuum mechanics, including linear elasticity theory and the solution of Stokes flows. It is written as
or
or
where  is the fourth power of the del operator and the square of the laplacian operator
is the fourth power of the del operator and the square of the laplacian operator  (or
(or  ), and it is known as the biharmonic operator or the bilaplacian operator.
), and it is known as the biharmonic operator or the bilaplacian operator.
For example, in three dimensional cartesian coordinates the biharmonic equation has the form
As another example, in n-dimensional Euclidean space,
where
which, for n=3 and n=5 only, becomes the biharmonic equation.
A solution to the biharmonic equation is called a biharmonic function. Any harmonic function is biharmonic, but the converse is not always true.
In two-dimensional polar coordinates, the biharmonic equation is
which can be solved by separation of variables. The result is the Michell solution.
2 dimensional space
The general solution to the 2 dimensional case is
where  ,
, 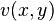 and
and 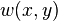 are harmonic functions and
are harmonic functions and 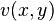 is a harmonic conjugate of
is a harmonic conjugate of  .
.
Just as harmonic functions in 2 variables are closely related to complex analytic functions, so are biharmonic functions in 2 variables. The general form of a biharmonic function in 2 variables can also be written as
where  and
and  are analytic functions.
are analytic functions.
See also
References
- Eric W Weisstein, CRC Concise Encyclopedia of Mathematics, CRC Press, 2002. ISBN 1-58488-347-2.
- S I Hayek, Advanced Mathematical Methods in Science and Engineering, Marcel Dekker, 2000. ISBN 0-8247-0466-5.
- J P Den Hartog (Jul 1, 1987). Advanced Strength of Materials. Courier Dover Publications. ISBN 0-486-65407-9.
External links
- Weisstein, Eric W., "Biharmonic Equation", MathWorld.
- Weisstein, Eric W., "Biharmonic Operator", MathWorld.