Bifurcation diagram

From Wikipedia, the free encyclopedia

In mathematics, particularly in dynamical systems, a bifurcation diagram shows the possible long-term values (equilibria/fixed points or periodic orbits) of a system as a function of a bifurcation parameter in the system. It is usual to represent stable solutions with a solid line and unstable solutions with a dotted line.

Bifurcations in 1D discrete dynamical systems

Logistic map

See also: Dynamical systems and List of chaotic maps

Bifurcation diagram of the logistic map

Animation showing the formation of bifurcation diagram

Bifurcation diagram of the circle map. Black regions correspond to Arnold tongues.

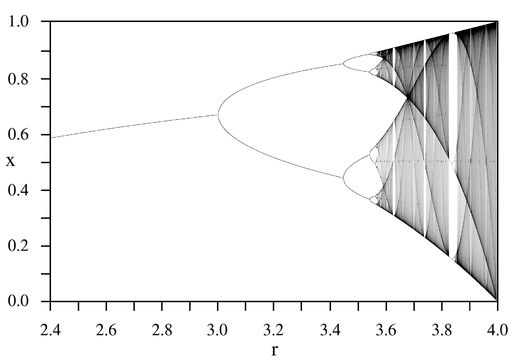
An example is the bifurcation diagram of the logistic map:

$x_{{n+1}}=rx_{n}(1-x_{n}).\,$

The bifurcation parameter r is shown on the horizontal axis of the plot and the vertical axis shows the possible long-term population values of the logistic function.

The bifurcation diagram nicely shows the forking of the possible periods of stable orbits from 1 to 2 to 4 to 8 etc. Each of these bifurcation points is a period-doubling bifurcation. The ratio of the lengths of successive intervals between values of r for which bifurcation occurs converges to the first Feigenbaum constant.

Real quadratic map

Symmetry breaking in bifurcation sets

Symmetry breaking in pitchfork bifurcation as the parameter epsilon is varied. epsilon = 0 is the case of symmetric pitchfork bifurcation.

In a dynamical system such as

${\ddot {x}}+f(x;\mu )+\epsilon g(x)=0$ ,

which is structurally stable when 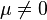$\mu \neq 0$ , if a bifurcation diagram is plotted, treating $\mu$ as the bifurcation parameter, but for different values of $\epsilon$ , the case $\epsilon =0$ is the symmetric pitchfork bifurcation. When $\epsilon \neq 0$ , we say we have a pitchfork with broken symmetry. This is illustrated in the animation on the right.

References

Paul Glendinning, "Stability, Instability and Chaos", Cambridge University Press, 1994.
Steven Strogatz, "Non-linear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering", Perseus Books, 2000.

External links

Logistic Map Simulation. A Java applet simulating the Logistic Map by Yuval Baror.
The Logistic Map and Chaos

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.