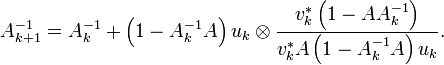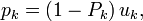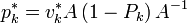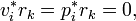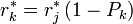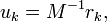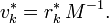Biconjugate gradient method
In mathematics, more specifically in numerical linear algebra, the biconjugate gradient method is an algorithm to solve systems of linear equations
Unlike the conjugate gradient method, this algorithm does not require the matrix 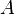 to be self-adjoint, but instead one needs to perform multiplications by the conjugate transpose <var>A</var>*.
to be self-adjoint, but instead one needs to perform multiplications by the conjugate transpose <var>A</var>*.
The algorithm
- Choose initial guess
 , two other vectors
, two other vectors 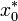 and
and 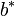 and a preconditioner
and a preconditioner 
-
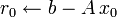
-

-
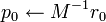
-
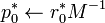
- for
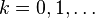 do
do
-
In the above formulation, the computed 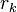 and
and 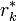 satisfy
satisfy
and thus are the respective residuals corresponding to 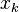 and
and  , as approximate solutions to the systems
, as approximate solutions to the systems
 is the adjoint, and
is the adjoint, and 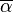 is the complex conjugate.
is the complex conjugate.
Unpreconditioned version of the algorithm
- Choose initial guess
 ,
, -
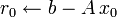
-
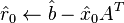
-
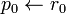
-
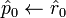
- for
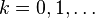 do
do
-
Discussion
The biconjugate gradient method is numerically unstable[citation needed] (compare to the biconjugate gradient stabilized method), but very important from a theoretical point of view. Define the iteration steps by
where  using the related projection
using the related projection
with
These related projections may be iterated themselves as
A relation to Quasi-Newton methods is given by 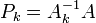 and
and  , where
, where
The new directions
are then orthogonal to the residuals:
which themselves satisfy
where  .
.
The biconjugate gradient method now makes a special choice and uses the setting
With this particular choice, explicit evaluations of 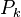 and <var>A</var>−1 are avoided, and the algorithm takes the form stated above.
and <var>A</var>−1 are avoided, and the algorithm takes the form stated above.
Properties
- If
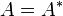 is self-adjoint,
is self-adjoint,  and
and 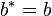 , then
, then 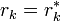 ,
, 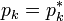 , and the conjugate gradient method produces the same sequence
, and the conjugate gradient method produces the same sequence 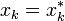 at half the computational cost.
at half the computational cost.
- The sequences produced by the algorithm are biorthogonal, i.e.,
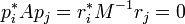 for
for  .
.
- if
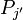 is a polynomial with
is a polynomial with 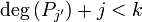 , then
, then 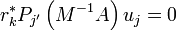 . The algorithm thus produces projections onto the Krylov subspace.
. The algorithm thus produces projections onto the Krylov subspace.
- if
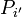 is a polynomial with
is a polynomial with  , then
, then  .
.
See also
References
- Fletcher, R. (1976). "Conjugate gradient methods for indefinite systems". In Watson, G. Alistair. Numerical Analysis. Lecture Notes in Mathematics (Springer Berlin / Heidelberg) 506: 73–89. doi:10.1007/BFb0080109. ISBN 978-3-540-07610-0. ISSN 1617-9692.
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 2.7.6". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8
| ||||||||||||||
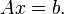
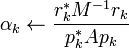
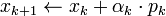
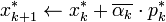
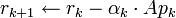
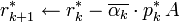
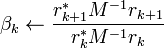
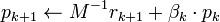
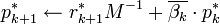
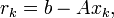

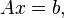
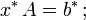
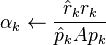
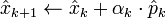

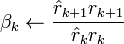
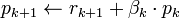
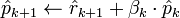
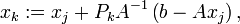

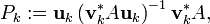
![{\mathbf {u}}_{k}=\left[u_{0},u_{1},\dots ,u_{{k-1}}\right],](/2014-wikipedia_en_all_02_2014/I/media/2/2/c/0/22c06621ecee4c38e89c6da91ddd8272.png)
![{\mathbf {v}}_{k}=\left[v_{0},v_{1},\dots ,v_{{k-1}}\right].](/2014-wikipedia_en_all_02_2014/I/media/6/8/5/5/6855792fc4a5a8f63e6aa232d35bb0e3.png)