Bi-twin chain

From Wikipedia, the free encyclopedia

In number theory, a bi-twin chain of length k + 1 is a sequence of natural numbers

$n-1,n+1,2n-1,2n+1,\dots ,2^{k}n-1,2^{k}n+1\,$

in which every number is prime.^[1]

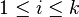The numbers $n-1,2n-1,\dots ,2^{k}n-1$ form a Cunningham chain of the first kind of length $k+1$ , while $n+1,2n+1,\dots ,2^{k}n+1$ forms a Cunningham chain of the second kind. Each of the pairs $2^{i}n-1,2^{i}n+1$ is a pair of twin primes. Each of the primes $2^{i}n-1$ for $0\leq i\leq k-1$ is a Sophie Germain prime and each of the primes $2^{i}n-1$ for $1\leq i\leq k$ is a safe prime.

Largest known bi-twin chains

Largest known bi-twin chains of length k + 1 (as of 22 January 2014^[2])
k	n	Digits	Year	Discoverer
0	3756801695685×2⁶⁶⁶⁶⁶⁹	200700	2011	Timothy D. Winslow, PrimeGrid
1	7317540034×5011#	2155	2012	Dirk Augustin
2	1329861957×937#×2³	399	2006	Dirk Augustin
3	223818083×409#×2⁶	177	2006	Dirk Augustin
4	39027761902802007714618528725397363585108921377235848032440823132447464787653697269×139#	138	2013	Primecoin (block 85429)
5	21011322942641319956617296739603541408400161540614555944797832220749394306836551×67#×2⁷	107	2014	Primecoin (block 383918)
6	227339007428723056795583×13#×2	29	2004	Torbjörn Alm & Jens Kruse Andersen
7	10739718035045524715×13#	24	2008	Jaroslaw Wroblewski
8	1873321386459914635×13#×2	24	2008	Jaroslaw Wroblewski

q# denotes the primorial 2×3×5×7×...×q.

As of 2014, the longest known bi-twin chain is of length 8.

Relation with other properties

Related chains

Cunningham chain

Related properties of primes/pairs of primes

Twin primes
Sophie Germain prime is a prime $p$ such that $2p+1$ is also prime.
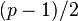Safe prime is a prime $p$ such that $(p-1)/2$ is also prime.

Notes and references

↑ Eric W. Weisstein, CRC Concise Encyclopedia of Mathematics, CRC Press, 2010, page 249.
↑ Henri Lifchitz, BiTwin records. Retrieved on 2014-01-22.

As of this edit, this article uses content from "Bitwin chain", which is licensed in a way that permits reuse under the Creative Commons Attribution-ShareAlike 3.0 Unported License, but not under the GFDL. All relevant terms must be followed.

v t e Prime number classes

By formula	Fermat (2^2ⁿ + 1) Mersenne (2^p − 1) Double Mersenne (2^{2^p−1} − 1) Wagstaff (2^p + 1)/3 Proth (k·2ⁿ + 1) Factorial (n! ± 1) Primorial (p_n# ± 1) Euclid (p_n# + 1) Pythagorean (4n + 1) Pierpont (2^u·3^v + 1) Solinas (2^a ± 2^b ± 1) Cullen (n·2ⁿ + 1) Woodall (n·2ⁿ − 1) Cuban (x³ − y³)/(x − y) Carol (2ⁿ − 1)² − 2 Kynea (2ⁿ + 1)² − 2 Leyland (x^y + y^x) Thabit (3·2ⁿ − 1) Mills (floor(A^3ⁿ))

By integer sequence	Fibonacci Lucas Motzkin Bell Partitions Pell Perrin Newman–Shanks–Williams

By property	Lucky Wall–Sun–Sun Wilson Wieferich Wieferich pair Fortunate Ramanujan Pillai Regular Strong Stern Supersingular (elliptic curve) Supersingular (moonshine theory) Wolstenholme Good Super Higgs Highly cototient Illegal

Base-dependent	Happy Dihedral Palindromic Emirp Repunit (10ⁿ − 1)/9 Permutable Circular Truncatable Strobogrammatic Minimal Full reptend Unique Primeval Self Smarandache–Wellin

Patterns	Twin (p, p + 2) Bi-twin chain (p − 1, p + 1, 2p − 1, 2p + 1, …) Triplet (p, p + 2 or p + 4, p + 6) Quadruplet (p, p + 2, p + 6, p + 8) Tuple Cousin (p, p + 4) Sexy (p, p + 6) Chen Sophie Germain (p, 2p + 1) Cunningham chain (p, 2p ± 1, …) Safe (p, (p − 1)/2) Arithmetic progression (p + a·n, n = 0, 1, …) Balanced (consecutive p − n, p, p + n)

By size	Titanic (1,000+ digits) Gigantic (10,000+) Mega (1,000,000+) Largest known

Complex numbers	Eisenstein prime Gaussian prime

Composite numbers	Pseudoprime Almost prime Semiprime Interprime

Related topics	Probable prime Industrial-grade prime Formula for primes Prime gap

List of prime numbers

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.