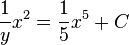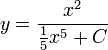Bernoulli differential equation
In mathematics, an ordinary differential equation of the form
is called a Bernoulli equation when n≠1, 0, which is named after Jacob Bernoulli, who discussed it in 1695 (Bernoulli 1695). Bernoulli equations are special because they are nonlinear differential equations with known exact solutions.
Solution
Let 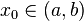 and
and
by a solution of the linear differential equation
Then we have that ![y(x):=[z(x)]^{{{\frac {1}{1-\alpha }}}}](/2014-wikipedia_en_all_02_2014/I/media/e/a/5/1/ea51c87d75b36b1c479829dbc4b88cc7.png) is a solution of
is a solution of
And for every such differential equation, for all 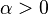 we have
we have 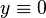 as solution for
as solution for 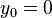 .
.
Example
Consider the Bernoulli equation (more specifically Riccati's equation).[1]
We first notice that  is a solution.
Division by
is a solution.
Division by  yields
yields
Changing variables gives the equations
which can be solved using the integrating factor
Multiplying by  ,
,
Note that left side is the derivative of  . Integrating both sides results in the equations
. Integrating both sides results in the equations
The solution for  is
is
as well as  .
.
References
- Bernoulli, Jacob (1695), "Explicationes, Annotationes & Additiones ad ea, quae in Actis sup. anni de Curva Elastica, Isochrona Paracentrica, & Velaria, hinc inde memorata, & paratim controversa legundur; ubi de Linea mediarum directionum, alliisque novis", Acta Eruditorum. Cited in Hairer, Nørsett & Wanner (1993).
- Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard (1993), Solving ordinary differential equations I: Nonstiff problems, Berlin, New York: Springer-Verlag, ISBN 978-3-540-56670-0.
- ↑ y'-2*y/x=-x^2*y^2, Wolfram Alpha, 01-06-2013
External links
- Bernoulli equation, PlanetMath.org.
- Differential equation, PlanetMath.org.
- Index of differential equations, PlanetMath.org.
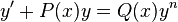
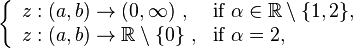

![y'(x)=P(x)y(x)+Q(x)y^{\alpha }(x)\ ,\ y(x_{0})=y_{0}:=[z(x_{0})]^{{{\frac {1}{1-\alpha }}}}.](/2014-wikipedia_en_all_02_2014/I/media/b/c/1/1/bc11e9c333fbb77df3a66adba493cfb9.png)
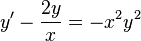

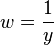
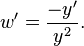

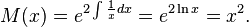
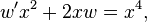
![\int d[wx^{2}]=\int x^{4}dx](/2014-wikipedia_en_all_02_2014/I/media/1/0/7/d/107d79bcf98a96bd200b49627fc4cd80.png)