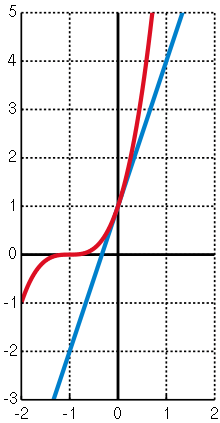
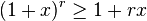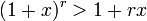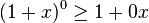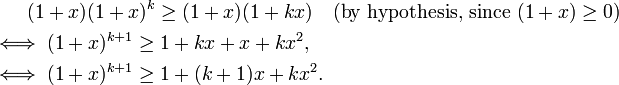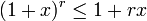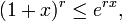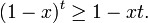Bernoulli's inequality
 and
and 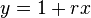 shown in red and blue respectively. Here,
shown in red and blue respectively. Here, 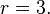
In real analysis, Bernoulli's inequality (named after Jacob Bernoulli) is an inequality that approximates exponentiations of 1 + x.
The inequality states that
for every integer r ≥ 0 and every real number x ≥ −1. If the exponent r is even, then the inequality is valid for all real numbers x. The strict version of the inequality reads
for every integer r ≥ 2 and every real number x ≥ −1 with x ≠ 0.
Bernoulli's inequality is often used as the crucial step in the proof of other inequalities. It can itself be proved using mathematical induction, as shown below.
Proof of the inequality
For r = 0,
is equivalent to 1 ≥ 1 which is true as required.
Now suppose the statement is true for r = k:
Then it follows that
However, as 1 + (k + 1)x + kx2 ≥ 1 + (k + 1)x (since kx2 ≥ 0), it follows that (1 + x)k + 1 ≥ 1 + (k + 1)x, which means the statement is true for r = k + 1 as required.
By induction we conclude the statement is true for all r ≥ 0.
Generalization
The exponent r can be generalized to an arbitrary real number as follows: if x > −1, then
for r ≤ 0 or r ≥ 1, and
for 0 ≤ r ≤ 1.
This generalization can be proved by comparing derivatives. Again, the strict versions of these inequalities require x ≠ 0 and r ≠ 0, 1.
Related inequalities
The following inequality estimates the r-th power of 1 + x from the other side. For any real numbers x, r > 0, one has
where e = 2.718.... This may be proved using the inequality (1 + 1/k)k < e.
Alternative form
An alternative form of Bernoulli's inequality for 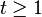 and
and  is:
is:
This can be proved (for integer t) by using the formula for geometric series: (using y=1-x)
or equivalently 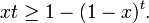
Proof for rational case
An "elementary" proof can be given using the fact that geometric mean of positive numbers is less than arithmetic mean
First assume 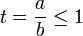
By comparing Arithmetic and Geometric mean of  numbers
(
numbers
(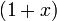 occurs
occurs  times):
times):

we get
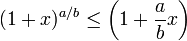
or equivalently
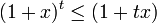
This proves inequality for  case.
case.
For  case,
let
case,
let  As
As 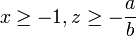 we get with
we get with 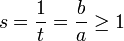 ,
,
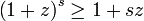
This proves inequality for  case.
case.
As these inequalities are true for all rational numbers  and
and  ,
they are also true for all real numbers. this is because, any real number can be
approximated by rational numbers to arbitrary precision (this formally follows from the Cauchy construction of real numbers).
,
they are also true for all real numbers. this is because, any real number can be
approximated by rational numbers to arbitrary precision (this formally follows from the Cauchy construction of real numbers).
References
- Carothers, N. (2000). Real Analysis. Cambridge: Cambridge University Press. p. 9. ISBN 978-0-521-49756-5.
- Bullen, P.S. (1987). Handbook of Means and Their Inequalities. Berlin: Springer. p. 4. ISBN 978-1-4020-1522-9.
- Zaidman, Samuel (1997). Advanced Calculus. City: World Scientific Publishing Company. p. 32. ISBN 978-981-02-2704-3.
External links
- Weisstein, Eric W., "Bernoulli Inequality", MathWorld.
- Bernoulli Inequality by Chris Boucher, Wolfram Demonstrations Project.
- Arthur Lohwater (1982). "Introduction to Inequalities". Online e-book in PDF format.
- Sanjeev Saxena, "A Simple Proof of Bernoulli's Inequality", viXra:1205.0068, May 2012