Bergman space

From Wikipedia, the free encyclopedia

In complex analysis, a branch of mathematics, a Bergman space, named after Stefan Bergman, is a function space of holomorphic functions in a domain D of the complex plane that are sufficiently well-behaved at the boundary that they are absolutely integrable. Specifically, 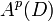$A^{p}(D)$ is the space of holomorphic functions in D such that the p-norm

$\|f\|_{p}=\left(\int _{D}|f(x+iy)|^{p}\,dx\,dy\right)^{{1/p}}<\infty .$

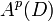Thus $A^{p}(D)$ is the subspace of holomorphic functions that are in the space L^p(D). The Bergman spaces are Banach spaces, which is a consequence of the estimate, valid on compact subsets K of D:

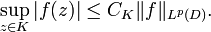
$\sup _{{z\in K}}|f(z)|\leq C_{K}\|f\|_{{L^{p}(D)}}.$

(1)

Thus convergence of a sequence of holomorphic functions in L^p(D) implies also compact convergence, and so the limit function is also holomorphic.

If p = 2, then 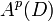$A^{p}(D)$ is a reproducing kernel Hilbert space, whose kernel is given by the Bergman kernel.

References

Bergman, Stefan (1970), The kernel function and conformal mapping, Mathematical Surveys 5 (2nd ed.), American Mathematical Society
Richter, Stefan (2001), "Bergman spaces", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 .
Hedenmalm, H.; Korenblum, B.; Zhu, K. (2000), Theory of Bergman Spaces, Springer, ISBN 978-0-387-98791-0

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.