Bending of plates
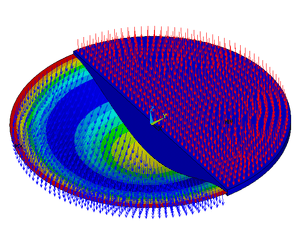
Bending of plates or plate bending refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the plate can be calculated from these deflections. Once the stresses are known, failure theories can be used to determine whether a plate will fail under a given load.
Bending of Kirchhoff-Love plates
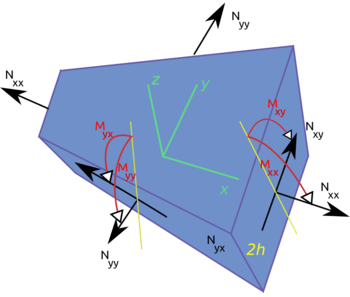
In the Kirchhoff–Love plate theory for plates the governing equations are[1]
and
In expanded form,
and
where 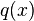 is an applied transverse load per unit area, the thickness of the plate is
is an applied transverse load per unit area, the thickness of the plate is  , the stresses are
, the stresses are 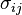 , and
, and
The quantity  has units of force per unit length. The quantity
has units of force per unit length. The quantity  has units of moment per unit length.
has units of moment per unit length.
For isotropic, homogeneous, plates with Young's modulus  and Poisson's ratio
and Poisson's ratio  these equations reduce to[2]
these equations reduce to[2]
where 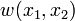 is the deflection of the mid-surface of the plate.
is the deflection of the mid-surface of the plate.
In rectangular Cartesian coordinates,
Circular Kirchhoff-Love plates
The bending of circular plates can be examined by solving the governing equation with appropriate boundary conditions. These solutions were first found by Poisson in 1829. Cylindrical coordinates are convenient for such problems.
The governing equation in coordinate-free form is
In cylindrical coordinates 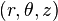 ,
,
For symmetrically loaded circular plates,  , and we have
, and we have
Therefore, the governing equation is
If  and
and  are constant, direct integration of the governing equation gives us
are constant, direct integration of the governing equation gives us
where 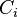 are constants. The slope of the deflection surface is
are constants. The slope of the deflection surface is
For a circular plate, the requirement that the deflection and the slope of the deflection are finite
at  implies that
implies that 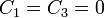 .
.
Clamped edges
For a circular plate with clamped edges, we have 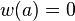 and
and  at the edge of
the plate (radius
at the edge of
the plate (radius  ). Using these boundary conditions we get
). Using these boundary conditions we get
The in-plane displacements in the plate are
The in-plane strains in the plate are
The in-plane stresses in the plate are
For a plate of thickness  , the bending stiffness is
, the bending stiffness is ![D=2Eh^{3}/[3(1-\nu ^{2})]](/2014-wikipedia_en_all_02_2014/I/media/e/9/3/f/e93f8cf55be54e5c7704e02d3da0e992.png) and we
have
and we
have
The moment resultants (bending moments) are
The maximum radial stress is at 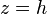 and
and  :
:
where 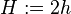 . The bending moments at the boundary and the center of the plate are
. The bending moments at the boundary and the center of the plate are
Rectangular Kirchhoff-Love plates

 per unit area.
per unit area.For rectangular plates, Navier in 1820 introduced a simple method for finding the displacement and stress when a plate is simply supported. The idea was to express the applied load in terms of Fourier components, find the solution for a sinusoidal load (a single Fourier component), and then superimpose the Fourier components to get the solution for an arbitrary load.
Sinusoidal load
Let us assume that the load is of the form
Here 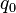 is the amplitude,
is the amplitude,  is the width of the plate in the
is the width of the plate in the  -direction, and
-direction, and
 is the width of the plate in the
is the width of the plate in the  -direction.
-direction.
Since the plate is simply supported, the displacement 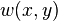 along the edges of
the plate is zero, the bending moment
along the edges of
the plate is zero, the bending moment  is zero at
is zero at  and
and  , and
, and
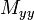 is zero at
is zero at  and
and 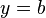 .
.
If we apply these boundary conditions and solve the plate equation, we get the solution
We can calculate the stresses and strains in the plate once we know the displacement.
For a more general load of the form
where  and
and  are integers, we get the solution
are integers, we get the solution
Navier solution
Let us now consider a more general load  . We can break this load up into
a sum of Fourier components such that
. We can break this load up into
a sum of Fourier components such that
where 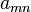 is an amplitude. We can use the orthogonality of Fourier components,
is an amplitude. We can use the orthogonality of Fourier components,
to find the amplitudes 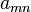 . Thus we have, by integrating over
. Thus we have, by integrating over  ,
,
If we repeat the process by integrating over  , we have
, we have
Therefore,
Now that we know 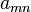 , we can just superpose solutions of the form given in
equation (1) to get the displacement, i.e.,
, we can just superpose solutions of the form given in
equation (1) to get the displacement, i.e.,
Uniform load
Consider the situation where a uniform load is applied on the plate, i.e.,
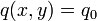 . Then
. Then
Now
We can use these relations to get a simpler expression for 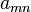 :
:
Since 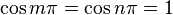 [ so
[ so  ] when
] when  and
and  are even, we can get an even simpler expression for
are even, we can get an even simpler expression for 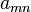 when both
when both  and
and  are odd:
are odd:
Plugging this expression into equation (2) and keeping in mind that only odd terms contribute to the displacement, we have
The corresponding moments are given by
The stresses in the plate are

 )
)

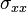 )
)

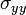 )
)
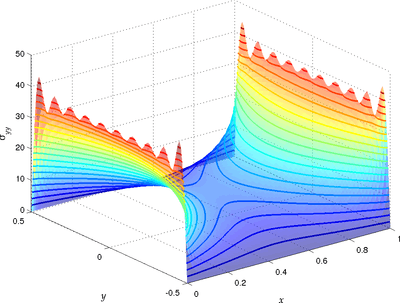
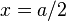 for a rectangular plate with
for a rectangular plate with  mm,
mm,  mm,
mm, 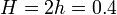 mm,
mm, 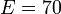 GPa, and
GPa, and 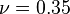 under a load
under a load 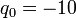 kPa. The red line represents the bottom of the plate, the green line the middle, and the blue line the top of the plate.
kPa. The red line represents the bottom of the plate, the green line the middle, and the blue line the top of the plate.
Levy solution
Another approach was proposed by Levy in 1899. In this case we start with an assumed form of the displacement and try to fit the parameters so that the governing equation and the boundary conditions are satisfied.
Let us assume that
For a plate that is simply supported at  and
and  , the boundary conditions
are
, the boundary conditions
are  and
and 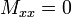 . The moment boundary condition is equivalent to
. The moment boundary condition is equivalent to
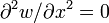 (verify). The goal is to find
(verify). The goal is to find 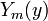 such that
it satisfies the boundary conditions at
such that
it satisfies the boundary conditions at  and
and 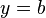 and, of course, the
governing equation
and, of course, the
governing equation  .
.
Moments along edges
Let us consider the case of pure moment loading. In that case 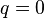 and
and
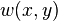 has to satisfy
has to satisfy 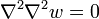 . Since we are working in rectangular
Cartesian coordinates, the governing equation can be expanded as
. Since we are working in rectangular
Cartesian coordinates, the governing equation can be expanded as
Plugging the expression for 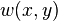 in the governing equation gives us
in the governing equation gives us
or
This is an ordinary differential equation which has the general solution
where 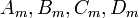 are constants that can be determined from the boundary
conditions. Therefore the displacement solution has the form
are constants that can be determined from the boundary
conditions. Therefore the displacement solution has the form
Let us choose the coordinate system such that the boundaries of the plate are
at  and
and  (same as before) and at
(same as before) and at 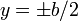 (and not
(and not  and
and
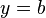 ). Then the moment boundary conditions at the
). Then the moment boundary conditions at the 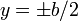 boundaries are
boundaries are
where 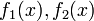 are known functions. The solution can be found by
applying these boundary conditions. We can show that for the symmetrical case
where
are known functions. The solution can be found by
applying these boundary conditions. We can show that for the symmetrical case
where
and
we have
where
Similarly, for the antisymmetrical case where
we have
We can superpose the symmetric and antisymmetric solutions to get more general solutions.
Uniform and symmetric moment load
For the special case where the loading is symmetric and the moment is uniform, we have at 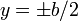 ,
,

 )
)
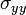 )
)

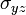 )
)
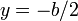 and
and 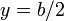 . The bending stress
. The bending stress 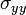 is along the bottom surface of the plate. The transverse shear stress
is along the bottom surface of the plate. The transverse shear stress 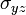 is along the mid-surface of the plate.
is along the mid-surface of the plate.
The resulting displacement is
where
The bending moments and shear forces corresponding to the displacement  are
are
The stresses are
Cylindrical plate bending
Cylindrical bending occurs when a rectangular plate that has dimensions  , where
, where 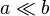 and the thickness
and the thickness  is small, is subjected to a uniform distributed load perpendicular to the plane of the plate. Such a plate takes the shape of the surface of a cylinder.
is small, is subjected to a uniform distributed load perpendicular to the plane of the plate. Such a plate takes the shape of the surface of a cylinder.
Simply supported plate with axially fixed ends
For a simply supported plate under cylindrical bending with edges that are free to rotate but have a fixed  . Cylindrical bending solutions can be found using the Navier and Levy techniques.
. Cylindrical bending solutions can be found using the Navier and Levy techniques.
Bending of thick Mindlin plates
For thick plates, we have to consider the effect of through-the-thickness shears on the orientation of the normal to the mid-surface after deformation. Mindlin's theory provides one approach for find the deformation and stresses in such plates. Solutions to Mindlin's theory can be derived from the equivalent Kirchhoff-Love solutions using canonical relations.[3]
Governing equations
The canonical governing equation for isotropic thick plates can be expressed as[3]
where  is the applied transverse load,
is the applied transverse load,  is the shear modulus,
is the shear modulus, ![D=Eh^{3}/[12(1-\nu ^{2})]](/2014-wikipedia_en_all_02_2014/I/media/9/1/7/0/91700a0a0e541fde0e46a1b0b959b10e.png) is the bending rigidity,
is the bending rigidity,  is the plate thickness,
is the plate thickness, ![c^{2}=2\kappa Gh/[D(1-\nu )]](/2014-wikipedia_en_all_02_2014/I/media/1/4/7/8/1478eb17dc1b4e68e7300d609140f013.png) ,
,
 is the shear correction factor,
is the shear correction factor,  is the Young's modulus,
is the Young's modulus,  is the Poisson's
ratio, and
is the Poisson's
ratio, and
In Mindlin's theory,  is the transverse displacement of the mid-surface of the plate
and the quantities
is the transverse displacement of the mid-surface of the plate
and the quantities 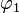 and
and  are the rotations of the mid-surface normal
about the
are the rotations of the mid-surface normal
about the 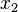 and
and  -axes, respectively. The canonical parameters for this theory
are
-axes, respectively. The canonical parameters for this theory
are  and
and 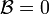 . The shear correction factor
. The shear correction factor  usually has the
value
usually has the
value  .
.
The solutions to the governing equations can be found if one knows the corresponding Kirchhoff-Love solutions by using the relations
where 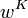 is the displacement predicted for a Kirchhoff-Love plate,
is the displacement predicted for a Kirchhoff-Love plate,  is a
biharmonic function such that
is a
biharmonic function such that  ,
, 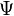 is a function that satisfies the
Laplace equation,
is a function that satisfies the
Laplace equation,  , and
, and
Simply supported rectangular plates
For simply supported plates, the Marcus moment sum vanishes, i.e.,
In that case the functions  ,
, 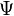 ,
,  vanish, and the Mindlin solution is
related to the corresponding Kirchhoff solution by
vanish, and the Mindlin solution is
related to the corresponding Kirchhoff solution by
Bending of Reissner-Stein cantilever plates
Reissner-Stein theory for cantilever plates[4] leads to the following coupled ordinary differential equations for a cantilever plate with concentrated end load 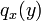 at
at  .
.
and the boundary conditions at  are
are
Solution of this system of two ODEs gives
where 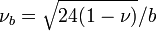 . The bending moments and shear forces corresponding to the displacement
. The bending moments and shear forces corresponding to the displacement
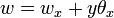 are
are
The stresses are
If the applied load at the edge is constant, we recover the solutions for a beam under a
concentrated end load. If the applied load is a linear function of  , then
, then
See also
- Bending
- Infinitesimal strain theory
- Kirchhoff–Love plate theory
- Linear elasticity
- Mindlin–Reissner plate theory
- Plate theory
- Stress (mechanics)
- Stress resultants
- Structural acoustics
- Vibration of plates
References
- ↑ Reddy, J. N., 2007, Theory and analysis of elastic plates and shells, CRC Press, Taylor and Francis.
- ↑ Timoshenko, S. and Woinowsky-Krieger, S., (1959), Theory of plates and shells, McGraw-Hill New York.
- ↑ 3.0 3.1 Lim, G. T. and Reddy, J. N., 2003, On canonical bending relationships for plates, International Journal of Solids and Structures, vol. 40, pp. 3039-3067.
- ↑ E. Reissner and M. Stein. Torsion and transverse bending of cantilever plates. Technical Note 2369, National Advisory Committee for Aeronautics,Washington, 1951.
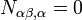
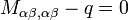
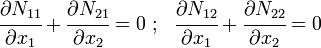
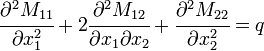
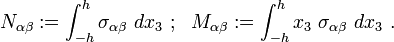

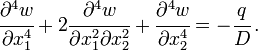

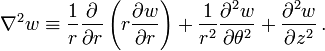
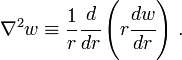
![{\frac {1}{r}}{\cfrac {d}{dr}}\left[r{\cfrac {d}{dr}}\left\{{\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\right\}\right]=-{\frac {q}{D}}\,.](/2014-wikipedia_en_all_02_2014/I/media/0/6/f/b/06fb2af0b5690fed73d532b7e5d10e27.png)
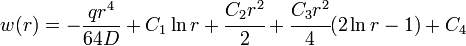
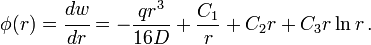

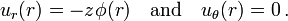
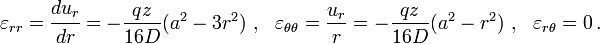
![\sigma _{{rr}}={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{{rr}}+\nu \varepsilon _{{\theta \theta }}\right]~;~~\sigma _{{\theta \theta }}={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{{\theta \theta }}+\nu \varepsilon _{{rr}}\right]~;~~\sigma _{{r\theta }}=0\,.](/2014-wikipedia_en_all_02_2014/I/media/3/5/7/7/3577b9730230ac1f793c6bbc0f0bab80.png)
![{\begin{aligned}\sigma _{{rr}}&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^{2}-(3+\nu )r^{2}\right]\\\sigma _{{\theta \theta }}&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]\\\sigma _{{r\theta }}&=0\,.\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/1/c/9/c/1c9c9adce33fd3b2fb63e289e0e87b59.png)
![M_{{rr}}=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(3+\nu )r^{2}\right]~;~~M_{{\theta \theta }}=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]~;~~M_{{r\theta }}=0\,.](/2014-wikipedia_en_all_02_2014/I/media/0/6/3/0/0630f29b87e995692973c0974f6e3ec6.png)
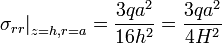

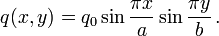
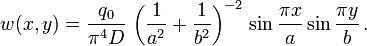

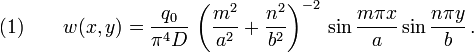

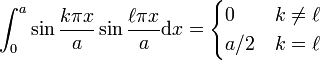
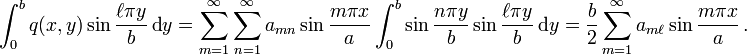

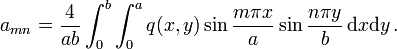
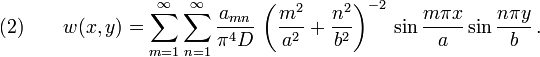
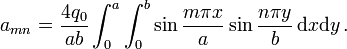
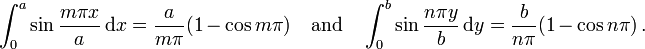


![{\begin{aligned}w(x,y)&=\sum _{{m=1}}^{\infty }\sum _{{n=1}}^{\infty }{\frac {16q_{0}}{(2m-1)(2n-1)\pi ^{6}D}}\,\left[{\frac {(2m-1)^{2}}{a^{2}}}+{\frac {(2n-1)^{2}}{b^{2}}}\right]^{{-2}}\,\times \\&\qquad \qquad \quad \sin {\frac {(2m-1)\pi x}{a}}\sin {\frac {(2n-1)\pi y}{b}}\,.\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/6/b/8/a/6b8a36bd45110cecec1bff6f2fc8db60.png)
![{\begin{aligned}M_{{xx}}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu {\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&=\sum _{{m=1}}^{\infty }\sum _{{n=1}}^{\infty }{\frac {16q_{0}}{(2m-1)(2n-1)\pi ^{4}}}\,\left[{\frac {(2m-1)^{2}}{a^{2}}}+\nu {\frac {(2n-1)^{2}}{b^{2}}}\right]\,\times \\&\qquad \qquad \left[{\frac {(2m-1)^{2}}{a^{2}}}+{\frac {(2n-1)^{2}}{b^{2}}}\right]^{{-2}}\sin {\frac {(2m-1)\pi x}{a}}\sin {\frac {(2n-1)\pi y}{b}}\\M_{{yy}}&=-D\left({\frac {\partial ^{2}w}{\partial y^{2}}}+\nu {\frac {\partial ^{2}w}{\partial x^{2}}}\right)\\&=\sum _{{m=1}}^{\infty }\sum _{{n=1}}^{\infty }{\frac {16q_{0}}{(2m-1)(2n-1)\pi ^{4}}}\,\left[{\frac {(2n-1)^{2}}{b^{2}}}+\nu {\frac {(2m-1)^{2}}{a^{2}}}\right]\,\times \\&\qquad \qquad \left[{\frac {(2m-1)^{2}}{a^{2}}}+{\frac {(2n-1)^{2}}{b^{2}}}\right]^{{-2}}\sin {\frac {(2m-1)\pi x}{a}}\sin {\frac {(2n-1)\pi y}{b}}\,.\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/c/7/6/7/c7672d4d3737248ceb6f3ca0605903ed.png)
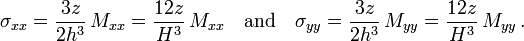
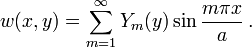
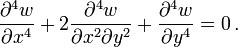
![\sum _{{m=1}}^{\infty }\left[\left({\frac {m\pi }{a}}\right)^{4}Y_{m}\sin {\frac {m\pi x}{a}}-2\left({\frac {m\pi }{a}}\right)^{2}{\cfrac {d^{2}Y_{m}}{dy^{2}}}\sin {\frac {m\pi x}{a}}+{\frac {d^{4}Y_{m}}{dy^{4}}}\sin {\frac {m\pi x}{a}}\right]=0](/2014-wikipedia_en_all_02_2014/I/media/4/a/7/6/4a76ec2ed445ae5523f122435bb6b27f.png)
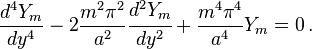

![w(x,y)=\sum _{{m=1}}^{\infty }\left[\left(A_{m}+B_{m}{\frac {m\pi y}{a}}\right)\cosh {\frac {m\pi y}{a}}+\left(C_{m}+D_{m}{\frac {m\pi y}{a}}\right)\sinh {\frac {m\pi y}{a}}\right]\sin {\frac {m\pi x}{a}}\,.](/2014-wikipedia_en_all_02_2014/I/media/2/2/9/4/22945cdc55837cf681863de0fb2c6a0b.png)

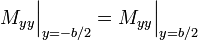
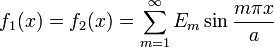
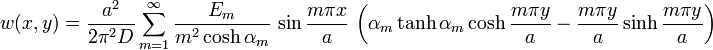
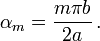
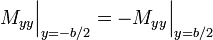
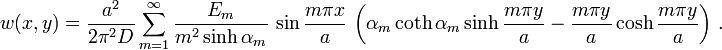

![{\begin{aligned}w(x,y)&={\frac {2M_{0}a^{2}}{\pi ^{3}D}}\sum _{{m=1}}^{\infty }{\frac {1}{(2m-1)^{3}\cosh \alpha _{m}}}\sin {\frac {(2m-1)\pi x}{a}}\times \\&\qquad \left[\alpha _{m}\,\tanh \alpha _{m}\cosh {\frac {(2m-1)\pi y}{a}}-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}\right]\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/b/8/6/e/b86ecb38c0ff733c1844bf3d3829705d.png)
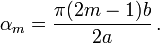
![{\begin{aligned}M_{{xx}}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&={\frac {2M_{0}(1-\nu )}{\pi }}\sum _{{m=1}}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\sin {\frac {(2m-1)\pi x}{a}}\left[-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.\left\{{\frac {2\nu }{1-\nu }}+\alpha _{m}\tanh \alpha _{m}\right\}\cosh {\frac {(2m-1)\pi y}{a}}\right]\\M_{{xy}}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&=-{\frac {2M_{0}(1-\nu )}{\pi }}\sum _{{m=1}}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\cos {\frac {(2m-1)\pi x}{a}}\left[{\frac {(2m-1)\pi y}{a}}\cosh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.(1-\alpha _{m}\tanh \alpha _{m})\sinh {\frac {(2m-1)\pi y}{a}}\right]\\Q_{{zx}}&={\frac {\partial M_{{xx}}}{\partial x}}-{\frac {\partial M_{{xy}}}{\partial y}}\\&={\frac {4M_{0}}{a}}\sum _{{m=1}}^{\infty }{\frac {1}{\cosh \alpha _{m}}}\,\cos {\frac {(2m-1)\pi x}{a}}\cosh {\frac {(2m-1)\pi y}{a}}\,.\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/5/1/8/0/518067cf05303ef5aed6b9e71aee1bb9.png)
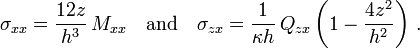
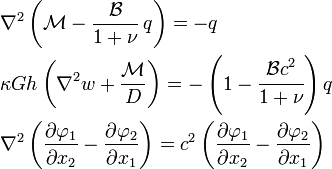
![{\mathcal {M}}=D\left[{\mathcal {A}}\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\frac {\partial \varphi _{2}}{\partial x_{2}}}\right)-(1-{\mathcal {A}})\nabla ^{2}w\right]+{\frac {2q}{1-\nu ^{2}}}{\mathcal {B}}\,.](/2014-wikipedia_en_all_02_2014/I/media/3/b/8/f/3b8fc8f025932daa1de6b1f088ffe07a.png)

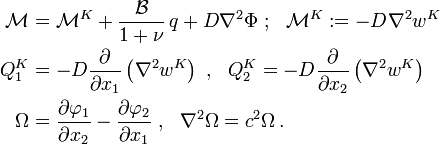
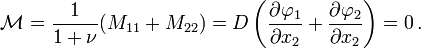
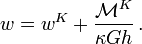
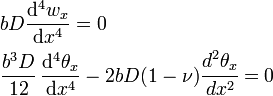
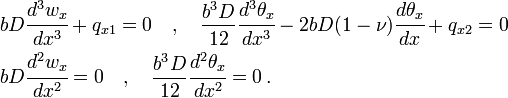
![{\begin{aligned}w_{x}(x)&={\frac {q_{{x1}}}{6bD}}\,(3ax^{2}-x^{3})\\\theta _{x}(x)&={\frac {q_{{x2}}}{2bD(1-\nu )}}\left[x-{\frac {1}{\nu _{b}}}\,\left({\frac {\sinh(\nu _{b}a)}{\cosh[\nu _{b}(x-a)]}}+\tanh[\nu _{b}(x-a)]\right)\right]\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/8/2/c/e/82ce61333e6f1deb825a2911d1ebc132.png)
![{\begin{aligned}M_{{xx}}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&=q_{{x1}}\left({\frac {x-a}{b}}\right)-\left[{\frac {3yq_{{x2}}}{b^{3}\nu _{b}\cosh ^{3}[\nu _{b}(x-a)]}}\right]\times \\&\quad \left[6\sinh(\nu _{b}a)-\sinh[\nu _{b}(2x-a)]+\sinh[\nu _{b}(2x-3a)]+8\sinh[\nu _{b}(x-a)]\right]\\M_{{xy}}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&={\frac {q_{{x2}}}{2b}}\left[1-{\frac {2+\cosh[\nu _{b}(x-2a)]-\cosh[\nu _{b}x]}{2\cosh ^{2}[\nu _{b}(x-a)]}}\right]\\Q_{{zx}}&={\frac {\partial M_{{xx}}}{\partial x}}-{\frac {\partial M_{{xy}}}{\partial y}}\\&={\frac {q_{{x1}}}{b}}-\left({\frac {3yq_{{x2}}}{2b^{3}\cosh ^{4}[\nu _{b}(x-a)]}}\right)\times \left[32+\cosh[\nu _{b}(3x-2a)]-\cosh[\nu _{b}(3x-4a)]\right.\\&\qquad \left.-16\cosh[2\nu _{b}(x-a)]+23\cosh[\nu _{b}(x-2a)]-23\cosh(\nu _{b}x)\right]\,.\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/d/0/5/a/d05ad2096e94ea6b8c0f62079f84a131.png)
