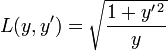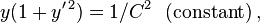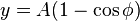Beltrami identity
The Beltrami identity is a simplified and less general version of the Euler-Lagrange equation in the calculus of variations.
The Euler-Lagrange equation serves to extremize action functionals of the form[1]
where a, b are constants and u′(x) = du / dx.
For the special case of ∂L / ∂x = 0, the Euler-Lagrange equation reduces to the Beltrami identity,[2]
where C is a constant. Thus, the Legendre transform of the Lagrangian, the Hamiltonian, is constant on the dynamical path.
Derivation
The following derivation of the Beltrami identity[3] starts with the Euler-Lagrange equation,
Multiplying both sides by u′,
According to the chain rule,
where u′′ = du′/dx = d2u / dx2.
Rearranging this yields
Thus, substituting this expression for u′ ∂L/∂u into the second equation of this derivation,
By the product rule, the last term is re-expressed as
and rearranging,
For the case of ∂L / ∂x = 0, this reduces to
so that taking the antiderivative results in the Beltrami identity,
where C is a constant.
Application
An example of an application of the Beltrami identity is the Brachistochrone problem, which involves finding the curve y = y(x) that minimizes the integral
The integrand
does not depend explicitly on the variable of integration x, so the Beltrami identity applies,
Substituting for L and simplifying,
which can be solved with the result put in the form of parametric equations
with A being half the above constant, 1/(2C ²), and φ being a variable. These are the parametric equations for a cycloid.[4]
References
- ↑ Courant R, Hilbert D (1953). Methods of Mathematical Physics. Vol. I (First English ed.). New York, New York: Interscience Publishers, Inc. p. 184. ISBN 978-0471504474.
- ↑ Weisstein, Eric W. "Euler-Lagrange Differential Equation." From MathWorld--A Wolfram Web Resource. See Eq. (5).
- ↑ This derivation of the Beltrami identity corresponds to the one at — Weisstein, Eric W. "Beltrami Identity." From MathWorld--A Wolfram Web Resource.
- ↑ This solution of the Brachistochrone problem corresponds to the one in — Mathews, Jon; Walker, RL (1965). Mathematical Methods of Physics. New York, New York: W. A. Benjamin, Inc. pp. 307–9.
![I[u]=\int _{a}^{b}L[x,u(x),u'(x)]\,dx\,,](/2014-wikipedia_en_all_02_2014/I/media/d/8/d/c/d8dc9ee147e2bdb31a1dd4ffdb2fef43.png)



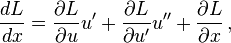





![I[y]=\int _{0}^{a}{\sqrt {{1+y'^{{\,2}}} \over y}}dx\,.](/2014-wikipedia_en_all_02_2014/I/media/3/7/1/5/3715084c9ad1a77f801f848f81535e1c.png)