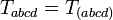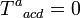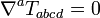Bel–Robinson tensor
In general relativity and differential geometry, the Bel–Robinson tensor is a tensor defined in the abstract index notation by:
Alternatively,
where  is the Weyl tensor. It was introduced by Lluis Bel in 1959.[1][2] The Bel–Robinson tensor is constructed from the Weyl tensor in a manner analogous to the way the electromagnetic stress–energy tensor is built from the electromagnetic tensor. Like the electromagnetic stress–energy tensor, the Bel–Robinson tensor is totally symmetric and traceless:
is the Weyl tensor. It was introduced by Lluis Bel in 1959.[1][2] The Bel–Robinson tensor is constructed from the Weyl tensor in a manner analogous to the way the electromagnetic stress–energy tensor is built from the electromagnetic tensor. Like the electromagnetic stress–energy tensor, the Bel–Robinson tensor is totally symmetric and traceless:
In general relativity, there is no unique definition of the local energy of the gravitational field. The Bel–Robinson tensor is a possible definition for local energy, since it can be shown that whenever the Ricci tensor vanishes (i.e. in vacuum), the Bel–Robinson tensor is divergence-free:
References
- ↑ Bel, L. (1959), "Introduction d'un tenseur du quatrième ordre", Comptes rendus hebdomadaires des séances de l'Académie des sciences 248: 1297
- ↑ Senovilla, J. M. M. (2000), "Editor's Note: Radiation States and the Problem of Energy in General Relativity by Louis Bel", General Relativity and Gravitation 32: 2043, doi:10.1023/A:1001906821162

![T_{{abcd}}=C_{{aecf}}C_{{b}}{}^{{e}}{}_{{d}}{}^{{f}}-{\frac {3}{2}}g_{{a[b}}C_{{jk]cf}}C^{{jk}}{}_{{d}}{}^{{f}}](/2014-wikipedia_en_all_02_2014/I/media/2/3/f/0/23f0e631e6756fbfb6c3c34054eba8fa.png)