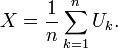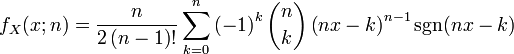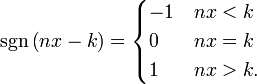Bates distribution

From Wikipedia, the free encyclopedia
Bates
Probability density function
No image available
Cumulative distribution function
No image available
Parameters 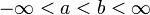-\infty <a<b<\infty \,
n\geq 1 integer
Support x\in [a,b]
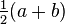Mean {\tfrac {1}{2}}(a+b)
Variance {\tfrac {1}{12n}}(b-a)^{2}
Skewness 0
Ex. kurtosis 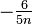-{\tfrac {6}{5n}}
CF 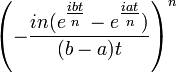\left(-{\frac {in(e^{{{\tfrac {ibt}{n}}}}-e^{{{\tfrac {iat}{n}}}})}{(b-a)t}}\right)^{n}

In probability and statistics, the Bates distribution, is a probability distribution of the mean of a number of statistically independent uniformly distributed random variables on the unit interval.[1] This distribution is sometimes confused with the Irwin–Hall distribution, which is the distribution of the sum (not mean) of n independent random variables uniformly distributed from 0 to 1.

Definition

The Bates distribution is the continuous probability distribution of the mean, X, of n independent uniformly distributed random variables on the unit interval, Ui:

X={\frac {1}{n}}\sum _{{k=1}}^{n}U_{k}.

The equation defining the probability density function of a Bates distribution random variable x is

f_{X}(x;n)={\frac {n}{2\left(n-1\right)!}}\sum _{{k=0}}^{{n}}\left(-1\right)^{k}{n \choose k}\left(nx-k\right)^{{n-1}}\operatorname{sgn}(nx-k)

for x in the interval (0,1), and zero elsewhere. Here sgn(x − k) denotes the sign function:

\operatorname{sgn} \left(nx-k\right)={\begin{cases}-1&nx<k\\0&nx=k\\1&nx>k.\end{cases}}

More generally, the mean of n independent uniformly distributed random variables on the interval [a,b]

X_{{(a,b)}}={\frac {1}{n}}\sum _{{k=1}}^{n}U_{k}(a,b).

would have the probability density function of

g(x;n,a,b)=f_{X}\left({\frac {x-a}{b-a}};n\right){\text{ for }}a\leq x\leq b\,

Notes

  1. ↑ Jonhson, N.L.; Kotz, S.; Balakrishnan (1995) Continuous Univariate Distributions, Volume 2, 2nd Edition, Wiley ISBN 0-471-58494-0(Section 26.9)

References

  • Bates,G.E. (1955) "Joint distributions of time intervals for the occurrence of successive accidents in a generalized Polya urn scheme", Annals of Mathematical Statistics, 26, 705–720
 
Continuous univariate supported on a bounded interval, e.g. [0,1]
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.