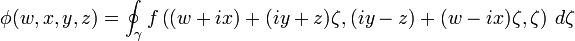Bateman transform
From Wikipedia, the free encyclopedia
In the mathematical study of partial differential equations, the Bateman transform is a method for solving the Laplace equation in four dimensions and wave equation in three by using a line integral of a holomorphic function in three complex variables. It is named after the English mathematician Harry Bateman, who first published the result in (Bateman 1904).
The formula asserts that if ƒ is a holomorphic function of three complex variables, then
is a solution of the Laplace equation, which follows by differentiation under the integral. Furthermore, Bateman asserted that the most general solution of the Laplace equation arises in this way.
References
- Bateman, Harry (1904), "The solution of partial differential equations by means of definite integrals", Proceedings of the London Mathematical Society 1 (1): 451–458, doi:10.1112/plms/s2-1.1.451.
- Eastwood, Michael (2002), Bateman's formula, MSRI.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.