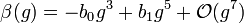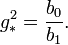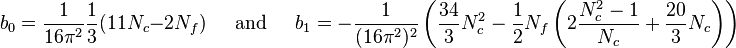Banks–Zaks fixed point
In quantum chromodynamics (and also N = 1 superquantum chromodynamics) with massless flavors, if the number of flavors, Nf, is sufficiently small (i.e. small enough to guarantee asymptotic freedom, depending on the number of colors), the theory can flow to an interacting conformal fixed point of the renormalization group. If the value of the coupling at that point is less than one (i.e. one can perform perturbation theory in weak coupling), then the fixed point is called a Banks–Zaks fixed point. The existence of the fixed point was first reported by William E. Caswell in 1974, and later used by Banks and Zaks in their analysis of the phase structure of vector-like gauge theories with massless fermions. For this reason one also justifiably finds references to a Caswell-Banks–Zaks fixed point.
More specifically, suppose that we find that the beta function of a theory up to two loops has the form
where 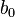 and
and  are positive constants. Then there exists a value
are positive constants. Then there exists a value 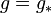 such that
such that 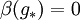 :
:
If we can arrange 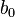 to be smaller than
to be smaller than  , then we have
, then we have 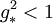 . It follows that when the theory flows to the IR it is a conformal, weakly coupled theory with coupling
. It follows that when the theory flows to the IR it is a conformal, weakly coupled theory with coupling 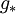 .
.
For the case of a non-Abelian gauge theory with gauge group 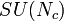 and Dirac fermions in the fundamental representation of the gauge group for the flavored particles we have
and Dirac fermions in the fundamental representation of the gauge group for the flavored particles we have
where  is the number of colors and
is the number of colors and 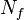 the number of flavors. Then
the number of flavors. Then 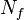 should lie just below
should lie just below 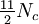 in order for the Banks–Zaks fixed point to appear. Note that this fixed point only occurs if, in addition to the previous requirement on
in order for the Banks–Zaks fixed point to appear. Note that this fixed point only occurs if, in addition to the previous requirement on 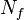 (which guarantees asymptotic freedom),
(which guarantees asymptotic freedom),
where the lower bound comes from requiring 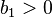 . This way
. This way  remains positive while
remains positive while 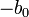 is still negative (see first equation in article) and one can solve
is still negative (see first equation in article) and one can solve 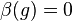 with real solutions for
with real solutions for 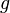 .
.
See also
References
- W. E. Caswell, Phys. Rev. Lett. 33 (1974) 244.
- T. Banks and A. Zaks, Nucl.Phys. B196, 189 (1982).