Band sum

From Wikipedia, the free encyclopedia

In geometric topology, a band sum of two n-dimensional knots K₁ and K₂ along an (n + 1)-dimensional 1-handle h called a band is an n-dimensional knot K such that:

There is an (n + 1)-dimensional 1-handle h connected to (K₁, K₂) embedded in S^n+2.
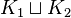There are points $p_{1}\in K_{1}$ and $p_{2}\in K_{2}$ such that $h$ is attached to $K_{1}\sqcup K_{2}$ along $p_{1}\sqcup p_{2}$ .

K is the n-dimensional knot obtained by this surgery.

A band sum is thus a generalization of the usual connected sum of knots.

See also

Manifold decomposition

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.