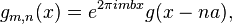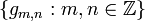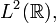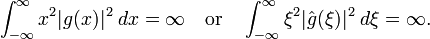Balian–Low theorem

From Wikipedia, the free encyclopedia

In mathematics, the Balian–Low theorem in Fourier analysis is named for Roger Balian and Francis E. Low. The theorem states that there is no well-localized window function (or Gabor atom) g either in time or frequency for an exact Gabor frame (Riesz Basis).

Suppose g is a square-integrable function on the real line, and consider the so-called Gabor system

g_{{m,n}}(x)=e^{{2\pi imbx}}g(x-na),

for integers m and n, and a,b>0 satisfying ab=1. The Balian–Low theorem states that if

\{g_{{m,n}}:m,n\in {\mathbb {Z}}\}

is an orthonormal basis for the Hilbert space

L^{2}({\mathbb {R}}),

then either

\int _{{-\infty }}^{\infty }x^{2}|g(x)|^{2}\;dx=\infty \quad {\textrm {or}}\quad \int _{{-\infty }}^{\infty }\xi ^{2}|{\hat {g}}(\xi )|^{2}\;d\xi =\infty .

The Balian–Low theorem has been extended to exact Gabor frames.

See also

References

  • Benedetto, John J.; Heil, Christopher; Walnut, David F. (1994). "Differentiation and the Balian–Low Theorem". Journal of Fourier Analysis and Applications 1 (4): 355–402. doi:10.1007/s00041-001-4016-5. 

This article incorporates material from Balian-Low on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.