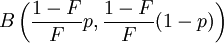Balding–Nichols model

From Wikipedia, the free encyclopedia

Balding-Nichols
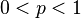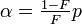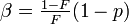Parameters	$0<F<1$ (real) $0<p<1$ (real) For ease of notation, let $\alpha ={\tfrac {1-F}{F}}p$ , and $\beta ={\tfrac {1-F}{F}}(1-p)$
Support	$x\in (0;1)\!$
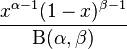pdf	${\frac {x^{{\alpha -1}}(1-x)^{{\beta -1}}}{{\mathrm {B}}(\alpha ,\beta )}}\!$
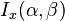CDF	$I_{x}(\alpha ,\beta )\!$
Mean	$p\!$
Median	$I_{{0.5}}^{{-1}}(\alpha ,\beta )$ no closed form
Mode	${\frac {F-(1-F)p}{3F-1}}$
Variance	$Fp(1-p)\!$
Skewness	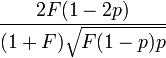${\frac {2F(1-2p)}{(1+F){\sqrt {F(1-p)p}}}}$
MGF	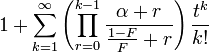$1+\sum _{{k=1}}^{{\infty }}\left(\prod _{{r=0}}^{{k-1}}{\frac {\alpha +r}{{\frac {1-F}{F}}+r}}\right){\frac {t^{k}}{k!}}$
CF	${}_{1}F_{1}(\alpha ;\alpha +\beta ;i\,t)\!$

In population genetics, the Balding–Nichols model is a statistical description of the allele frequencies in the components of a sub-divided population.^[1] With background allele frequency p the allele frequencies, in sub-populations separated by Wright's F_ST F, are distributed according to independent draws from

$B\left({\frac {1-F}{F}}p,{\frac {1-F}{F}}(1-p)\right)$

where B is the Beta distribution. This distribution has mean p and variance Fp(1 – p).^[2]

The model is due to David Balding and Richard Nichols and is widely used in the forensic analysis of DNA profiles and in population models for genetic epidemiology.

References

↑ Balding, DJ; Nichols, RA (1995). "A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity.". Genetica (Springer) 96: 3–12. doi:10.1007/BF01441146. PMID 7607457.
↑ Alkes L. Price, Nick J. Patterson, Robert M. Plenge, Michael E. Weinblatt, Nancy A. Shadick & David Reich (2006). "Principal components analysis corrects for stratification in genome-wide association studies" (PDF). Nature Genetics 38 (8): 904–909. doi:10.1038/ng1847. PMID 16862161.

v t e Population genetics

Key concepts	Hardy-Weinberg law Genetic linkage Identity by descent Linkage disequilibrium Fisher's fundamental theorem Neutral theory Price equation

Selection	Natural Sexual Artificial Ecological

Effects of selection on genomic variation	Genetic hitchhiking Background selection

Genetic drift	Small population size Population bottleneck Founder effect Coalescence Balding–Nichols model

Founders	R. A. Fisher J. B. S. Haldane Sewall Wright

Related topics	Evolution Microevolution Evolutionary game theory Fitness landscape Genetic genealogy

List of evolutionary biology topics

Probability distributions

Discrete univariate with finite support

Benford Bernoulli Beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot

Discrete univariate with infinite support

beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta

Continuous univariate supported on a bounded interval, e.g. [0,1]

Arcsine ARGUS Balding–Nichols Bates Beta Beta rectangular Irwin–Hall Kumaraswamy logit-normal Noncentral beta raised cosine Triangular U-quadratic uniform Wigner semicircle Xenakis

[[List of probability distributions#Supported_on_semi-infinite_intervals.2C_usually_.5B0.2C.E2.88.9E.29|Continuous univariate supported on a semi-infinite interval, usually [0,∞)]]

Benini
Benktander 1st kind
Benktander 2nd kind
Beta prime
Burr
chi-squared
chi
Coxian
Dagum
Davis
EL
Erlang
exponential
F
folded normal
Flory-Schulz
Fréchet
Gamma
Gamma/Gompertz
generalized inverse Gaussian
Gompertz
half-logistic
half-normal
Hotelling's T-squared
hyper-Erlang
hyperexponential
hypoexponential
inverse chi-squared (scaled inverse chi-squared)
inverse Gaussian
inverse gamma
Kolmogorov
Lévy
log-Cauchy
log-Laplace
log-logistic
log-normal
Maxwell–Boltzmann
Maxwell–Jüttner
Mittag–Leffler
Nakagami
noncentral chi-squared
Pareto
phase-type
Poly-Weibull
Rayleigh
relativistic Breit–Wigner
Rice
Rosin–Rammler
shifted Gompertz
truncated normal
type-2 Gumbel
Weibull
Wilks' lambda

Continuous univariate supported on the whole real line (−∞, ∞)

Cauchy exponential power Fisher's z generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson SU Landau Laplace Linnik logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel variance-gamma Voigt

Continuous univariate with support whose type varies

generalized extreme value generalized Pareto Tukey lambda q-Gaussian q-exponential shifted log-logistic

Mixed continuous-discrete univariate distributions

rectified Gaussian

Multivariate (joint)

Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet Generalized Dirichlet multivariate normal Multivariate stable multivariate Student normal-scaled inverse gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart

Directional

Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham

Degenerate and singular

Degenerate discrete degenerate Dirac delta function Singular Cantor

Families

Circular compound Poisson elliptical exponential natural exponential location-scale maximum entropy mixture Pearson Tweedie wrapped

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.