Bach tensor

From Wikipedia, the free encyclopedia

In differential geometry and general relativity, the Bach tensor is a trace-free tensor of rank 2 which is conformally invariant in dimension n = 4.[1] Before 1968, it was the only known conformally invariant tensor that is algebraically independent of the Weyl tensor.[2] In abstract indices the Bach tensor is given by

B_{{ab}}=P_{{cd}}{{{W_{a}}^{c}}_{b}}^{d}+\nabla ^{c}\nabla _{a}P_{{bc}}-\nabla ^{c}\nabla _{c}P_{{ab}}

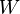where W is the Weyl tensor, and P the Schouten tensor given in terms of the Ricci tensor R_{{ab}} and scalar curvature R by

P_{{ab}}={\frac {1}{n-2}}\left(R_{{ab}}-{\frac {R}{2(n-1)}}g_{{ab}}\right).

See also

References

  1. ↑ Rudolf Bach, "Zur Weylschen Relativitätstheorie und der Weylschen Erweiterung des Krümmungstensorbegriffs", Mathematische Zeitschrift, 9 (1921) pp. 110.
  2. ↑ P. Szekeres, Conformal Tensors. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences Vol. 304, No. 1476 (Apr. 2, 1968), pp. 113–122

Further reading

  • Arthur L. Besse, Einstein Manifolds. Springer-Verlag, 2007. See Ch.4, §H "Quadratic Functionals".
  • Demetrios Christodoulou, Mathematical Problems of General Relativity I. European Mathematical Society, 2008. Ch.4 §2 "Sketch of the proof of the global stability of Minkowski spacetime".
  • Yvonne Choquet-Bruhat, General Relativity and the Einstein Equations. Oxford University Press, 2011. See Ch.XV §5 "Christodoulou-Klainerman theorem" which notes the Bach tensor is the "dual of the Coton tensor which vanishes for conformally flat metrics".
  • Thomas W. Baumgarte, Stuart L. Shapiro, Numerical Relativity: Solving Einstein's Equations on the Computer. Cambridge University Press, 2010. See Ch.3.


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.