B Integral
In nonlinear optics, B-Integral is a measure of the nonlinear phase shift of light. It calculates the exponential growth of the least stable spatial frequency in a laser beam, and is the numerical equivalent of the nonlinear phase shift along the laser system's optical axis.
In a multipass laser system as a cumulative measure of the nonlinear interaction,[1] this integral is given by:
where 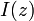 is the optical intensity along the beam axis,
is the optical intensity along the beam axis,  the position in beam direction, and
the position in beam direction, and  the nonlinear index quantifying the Kerr nonlinearity. As
the nonlinear index quantifying the Kerr nonlinearity. As 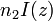 is the nonlinear change in the refractive index, one easily recognizes the B integral to be the total on-axis nonlinear phase shift accumulated in a passage through the device.
The B integral is frequently used in the context of ultrafast amplifiers, e.g. for optical components such as the Pockels cell of a regenerative amplifier.
is the nonlinear change in the refractive index, one easily recognizes the B integral to be the total on-axis nonlinear phase shift accumulated in a passage through the device.
The B integral is frequently used in the context of ultrafast amplifiers, e.g. for optical components such as the Pockels cell of a regenerative amplifier.
See also
References
- ↑ "B Integral". Encyclopedia of Laser Physics and Technology.
