BK-tree

From Wikipedia, the free encyclopedia

A BK-tree is a metric tree suggested by Walter Austin Burkhard and Robert M. Keller specifically adapted to discrete metric spaces. For simplicity, let us consider integer discrete metric 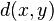$d(x,y)$ . Then, BK-tree is defined in the following way. An arbitrary element a is selected as root node. The root node may have zero or more subtrees. The k-th subtree is recursively built of all elements b such that 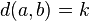$d(a,b)=k$ . BK-trees can be used for approximate string matching in a dictionary .

References

^ W. Burkhard and R. Keller. Some approaches to best-match file searching, CACM, 1973
^ R. Baeza-Yates, W. Cunto, U. Manber, and S. Wu. Proximity matching using fixed queries trees. In M. Crochemore and D. Gusfield, editors, 5th Combinatorial Pattern Matching, LNCS 807, pages 198-212, Asilomar, CA, June 1994.
^ Ricardo Baeza-Yates and Gonzalo Navarro. Fast Approximate String Matching in a Dictionary. Proc. SPIRE'98

External links

A BK-tree implementation in Common Lisp with test results and performance graphs.
An explanation of BK-Trees and their relationship to metric spaces

v t e Tree data structures

Binary trees	Binary search tree (BST) Cartesian tree MVP Tree Top tree T-tree Left-child right-sibling binary tree

Self-balancing binary search trees	AA tree AVL tree LLRB tree Red–black tree Scapegoat tree Splay tree Treap

B-trees	B+ tree B*-tree B^x-tree UB-tree 2–3 tree 2–3–4 tree (a,b)-tree Dancing tree HTree

Tries	Suffix tree Radix tree Hash tree Ternary search tree X-fast trie Y-fast trie

Binary space partitioning (BSP) trees	Quadtree Octree k-d tree Implicit k-d tree VP tree

Non-binary trees	Exponential tree Fusion tree Interval tree PQ tree Range tree SPQR tree Van Emde Boas tree

Spatial data partitioning trees	R-tree R+ tree R* tree X-tree M-tree Segment tree Hilbert R-tree Priority R-tree

Other trees	Heap Hash calendar Merkle tree Finger tree Order statistic tree Metric tree Cover tree BK-tree Doubly chained tree iDistance Link/cut tree Fenwick tree Log-structured merge-tree

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.