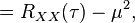Autocovariance
In statistics, given a real stochastic process X(t), the autocovariance is the covariance of the variable against a time-shifted version of itself. If the process has the mean ![E[X_{t}]=\mu _{t}](/2014-wikipedia_en_all_02_2014/I/media/f/4/b/c/f4bc2c1a0db78538f9fdf806bfcb679d.png) , then the autocovariance is given by
, then the autocovariance is given by
where E is the expectation operator.
Autocovariance is related to the more commonly used autocorrelation by the variance of the variable in question.
Stationarity
If X(t) is stationary process, then the following are true:
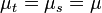 for all t, s
for all t, s
and
where
is the lag time, or the amount of time by which the signal has been shifted.
As a result, the autocovariance becomes
Normalization
When normalized by dividing by the variance σ2, the autocovariance C becomes the autocorrelation coefficient function c,[1]
However, often the autocovariance is called autocorrelation even if this normalization has not been performed.
The autocovariance can be thought of as a measure of how similar a signal is to a time-shifted version of itself with an autocovariance of σ2 indicating perfect correlation at that lag. The normalization with the variance will put this into the range [−1, 1].
Properties
The autocovariance of a linearly filtered process 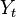
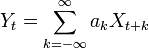
- is
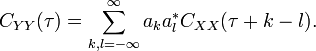
See also
References
- P. G. Hoel, Mathematical Statistics, Wiley, New York, 1984.
- Lecture notes on autocovariance from WHOI
- ↑ Westwick, David T. (2003). Identification of Nonlinear Physiological Systems. IEEE Press. pp. 17–18. ISBN 0-471-27456-9.
![C_{{XX}}(t,s)=E[(X_{t}-\mu _{t})(X_{s}-\mu _{s})]=E[X_{t}X_{s}]-\mu _{t}\mu _{s}.\,](/2014-wikipedia_en_all_02_2014/I/media/2/8/0/a/280a7a52105cda9a719e6ce0e0c144da.png)
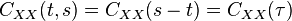

![C_{{XX}}(\tau )=E[(X(t)-\mu )(X(t+\tau )-\mu )]\,](/2014-wikipedia_en_all_02_2014/I/media/0/a/0/f/0a0f0b0322067c9d8ae3f934a2cf0dcb.png)
![=E[X(t)X(t+\tau )]-\mu ^{2}\,](/2014-wikipedia_en_all_02_2014/I/media/c/b/5/2/cb52602daac4d4c667f5e678b70076d1.png)