Aronszajn tree
In set theory, an Aronszajn tree is an uncountable tree with no uncountable branches and no uncountable levels. For example, every Suslin tree is an Aronszajn tree. More generally, for a cardinal κ, a κ-Aronszajn tree is a tree of height κ such that all levels have size less than κ and all branches have height less than κ (so Aronszajn trees are the same as 
-Aronszajn trees). They are named for Nachman Aronszajn, who constructed an Aronszajn tree in 1934.
A cardinal κ for which no κ-Aronszajn trees exist is said to have the tree property. (Sometimes the condition that κ is regular and uncountable is included.)
Existence of κ-Aronszajn trees
König's lemma states that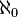 
-Aronszajn trees do not exist.
The existence of Aronszajn trees (=-Aronszajn trees) was proven by Nachman Aronszajn, and implies that the analogue of König's lemma does not hold for uncountable trees.
The existence of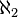 
-Aronszajn trees is undecidable (assuming a certain large cardinal axiom): more precisely, the continuum hypothesis implies the existence of an 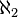-Aronszajn tree, and Mitchell and Silver showed that it is consistent (relative to the existence of a weakly compact cardinal) that no 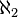-Aronszajn trees exist.
Jensen proved that V=L implies that there is a κ-Aronszajn tree (in fact a κ-Suslin tree) for every infinite successor cardinal κ.
Cummings & Foreman (1998) showed (using a large cardinal axiom) that it is consistent that no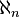 
-Aronszajn trees exist for any finite n other than 1.
If κ is weakly compact then no κ-Aronszajn trees exist. Conversely if κ is inaccessible and no κ-Aronszajn trees exist then κ is weakly compact.
Special Aronszajn trees
An Aronszajn tree is called special if there is a function f from the tree to the rationals so that
f(x)<f(y) whenever x<y. Martin's axiom MA() implies that all Aronszajn trees are special. The stronger proper forcing axiom implies the stronger statement that for any two Aronszajn trees there is a club set of levels such that the restrictions of the trees to this set of levels are isomorphic, which says that in some sense any two Aronszajn trees are essentially isomorphic. On the other hand, it is consistent that non-special Aronszajn trees exist, and this is also consistent with the generalized continuum hypothesis and with the Suslin hypothesis (Schlindwein 1994).
References
- Cummings, James; Foreman, Matthew (1998), "The tree property", Adv. Math. 133 (1): 1–32, doi:10.1006/aima.1997.1680, MR 1492784
- Schlindwein, Chaz (1994), "Consistency of Suslin's Hypothesis, A Nonspecial Aronszajn Tree, and GCH", The Journal of Symbolic Logic (The Journal of Symbolic Logic, Vol. 59, No. 1) 59 (1): 1–29, doi:10.2307/2275246, JSTOR 2275246
- Schlindwein, Ch. (2001), "A/a110690", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4