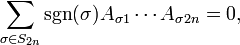Amitsur–Levitzki theorem
In algebra, the Amitsur–Levitzki theorem states that the algebra of n by n matrices satisfies a certain identity of degree 2n. It was proved by Amitsur and Levitsky (1950). In particular matrix rings are PI rings such that the smallest identity they satisfy has degree exactly 2n.
Statement
If A1,...,A2n are n by n matrices then
where the sum is over all (2n)! elements of the symmetric group S2n. (This polynomial is called the standard polynomial of degree 2n.)
Proofs
Amitsur and Levitzki (1950) gave the first proof.
Kostant (1958) deduced the Amitsur–Levitzki theorem from the Koszul–Samelson theorem about primitive cohomology of Lie algebras.
Swan (1963) and Swan (1969) gave a simple combinatorial proof as follows. By linearity it is enough to prove the theorem when each matrix has only one nonzero entry, which is 1. In this case each matrix can be encoded as a directed edge of a graph with n vertices. So all matrices together give a graph on n vertices with 2n directed edges. The identity holds provided that for any two vertices A and B of the graph, the number of odd Eulerian paths from A to B is the same as the number of even ones. (Here a path is called odd or even depending on whether its edges taken in order give an odd or even permutation of the 2n edges.) Swan showed that this was the case provided the number of edges in the graph is at least 2n, thus proving the Amitsur–Levitzki theorem.
Razmyslov (1974) gave a proof related to the Cayley–Hamilton theorem.
Rosset (1976) gave a short proof using the exterior algebra of a vector space of dimension 2n.
References
- Amitsur, A. S.; Levitzki, Jakob (1950), "Minimal identities for algebras", Proceedings of the American Mathematical Society 1: 449–463, doi:10.1090/S0002-9939-1950-0036751-9, ISSN 0002-9939, JSTOR 2032312, MR 0036751
- Amitsur, A. S.; Levitzki, Jakob (1951), "Remarks on Minimal identities for algebras", Proceedings of the American Mathematical Society 2: 320–327, ISSN 0002-9939, JSTOR 2032509, MR ?
- Formanek, E. (2001), "Amitsur–Levitzki theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Kostant, Bertram (1958), "A theorem of Frobenius, a theorem of Amitsur–Levitski and cohomology theory", J. Math. Mech. 7: 237–264, doi:10.1512/iumj.1958.7.07019, MR 0092755
- Razmyslov, Ju. P. (1974), "Identities with trace in full matrix algebras over a field of characteristic zero", Mathematics of the USSR-Izvestiya 8 (4): 727, doi:10.1070/IM1974v008n04ABEH002126, ISSN 0373-2436, MR 0506414
- Rosset, Shmuel (1976), "A new proof of the Amitsur–Levitski identity", Israel Journal of Mathematics 23 (2): 187–188, doi:10.1007/BF02756797, ISSN 0021-2172, MR 0401804
- Swan, Richard G. (1963), "An application of graph theory to algebra", Proceedings of the American Mathematical Society 14: 367–373, ISSN 0002-9939, JSTOR 2033801, MR 0149468
- Swan, Richard G. (1969), "Correction to "An application of graph theory to algebra"", Proceedings of the American Mathematical Society 21: 379–380, ISSN 0002-9939, JSTOR ?, MR 0255439