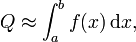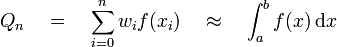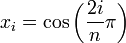Adaptive quadrature

From Wikipedia, the free encyclopedia

In applied mathematics, adaptive quadrature is a process in which the integral of a function $f(x)$ is approximated using static quadrature rules on adaptively refined subintervals of the integration domain. Generally, adaptive algorithms are just as efficient and effective as traditional algorithms for "well-behaved" integrands, but are also effective for "badly-behaved" integrands for which traditional algorithms fail.

General scheme

Adaptive quadrature follows the general scheme

1. procedure integrate ( f , a , b , tau )
2.    
3.    
4.    if  then
5.       m = (a + b) / 2
6.       Q = integrate(f,a,m,tau/2) + integrate(f,m,b,tau/2)
7.    endif
8.    return Q

An approximation $Q$ to the integral of $f(x)$ over the interval $[a,b]$ is computed (line 2), as well as an error estimate $\varepsilon$ (line 3). If the estimated error is larger than the required tolerance $\tau$ (line 4), the interval is subdivided (line 5) and the quadrature is applied on both halves separately (line 6). Either the initial estimate or the sum of the recursively computed halves is returned (line 7).

The important components are the quadrature rule itself

$Q\approx \int _{a}^{b}f(x)\,{\mbox{d}}x,$

the error estimator

$\varepsilon \approx \left|Q-\int _{a}^{b}f(x)\,{\mbox{d}}x\right|,$

and the logic for deciding which interval to subdivide, and when to terminate.

There are, of course, several variants of this scheme. The most common will be discussed later.

Basic quadrature rules

The quadrature rules generally have the form

$Q_{n}\quad =\quad \sum _{{i=0}}^{n}w_{i}f(x_{i})\quad \approx \quad \int _{a}^{b}f(x)\,{\mbox{d}}x$

where the nodes $x_{i}$ and weights $w_{i}$ are generally pre-computed.

In the simplest case, Newton–Cotes formulas of even degree are used, where the nodes $x_{i}$ are evenly spaced in the interval:

$x_{i}=a+{\frac {i}{n}}(b-a)$ .

When such rules are used, the points at which $f(x)$ has been evaluated can be re-used upon recursion:

A similar strategy is used with Clenshaw–Curtis quadrature, where the nodes are chosen as

$x_{i}=\cos \left({\frac {2i}{n}}\pi \right)$

Or, when Fejér quadrature is used,

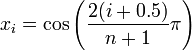$x_{i}=\cos \left({\frac {2(i+0.5)}{n+1}}\pi \right)$ .

Other quadrature rules, such as Gaussian quadrature or Gauss-Kronrod quadrature, may also be used.

An algorithm may elect to use different quadrature methods on different subintervals, for example using a high-order method only where the integrand is smooth.

Error estimation

Some quadrature algorithms generate a sequence of results which should approach the correct value. Otherwise one can use a "null rule" which has the form of the above quadrature rule, but whose value would be zero for a simple integrand (for example, if the integrand were a polynomial of the appropriate degree).

See:

Richardson extrapolation (see also Romberg's method)
Null rules
Epsilon algorithm

Subdivision logic

"Local" adaptive quadrature makes the acceptable error for a given interval proportional to the length of that interval. This criterion can be difficult to satisfy if the integrand are badly behaved at only a few points, for example with a few step discontinuities. Alternatively, one could require only that the sum of the errors on each of the subintervals be less than the user's requirement. This would be "global" adaptive quadrature. Global adaptive quadrature can be more efficient (using fewer evaluations of the integrand) but are generally more complex to program and may require more working space to record information on the current set of intervals.

References

William M. McKeeman: Algorithm 145: Adaptive numerical integration by Simpson's rule. Commun. ACM 5(12): 604 (1962).
John R. Rice. A Metalgorithm for Adaptive Quadrature. Journal of the ACM 22(1) pp 61-82 (January 1975).
Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 4.7. Adaptive Quadrature", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.