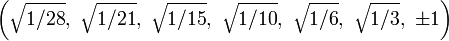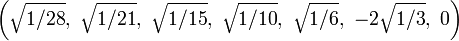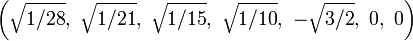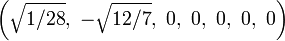7-simplex

From Wikipedia, the free encyclopedia

Regular octaexon (7-simplex)
Model created using straws (edges) and plasticine balls (vertices) in triakis tetrahedral envelope
Type	Regular 7-polytope
Family	simplex
Schläfli symbol	{3,3,3,3,3,3}
Coxeter-Dynkin diagram
6-faces	8 6-simplex
5-faces	28 5-simplex
4-faces	56 5-cell
Cells	70 tetrahedron
Faces	56 triangle
Edges	28
Vertices	8
Vertex figure	6-simplex
Petrie polygon	octagon
Coxeter group	A₇ [3,3,3,3,3,3]
Dual	Self-dual
Properties	convex

In 7-dimensional geometry, a 7-simplex is a self-dual regular 7-polytope. It has 8 vertices, 28 edges, 56 triangle faces, 70 tetrahedral cells, 56 5-cell 5-faces, 28 5-simplex 6-faces, and 8 6-simplex 7-faces. Its dihedral angle is cos⁻¹(1/7), or approximately 81.79°.

Alternate names

It can also be called an octaexon, or octa-7-tope, as an 8-facetted polytope in 7-dimensions. The name octaexon is derived from octa for eight facets in Greek and -ex for having six-dimensional facets, and -on. Jonathan Bowers gives an octaexon the acronym oca.^[1]

Coordinates

The Cartesian coordinates of the vertices of an origin-centered regular octaexon having edge length 2 are:

$\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ {\sqrt {1/3}},\ \pm 1\right)$

$\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ -2{\sqrt {1/3}},\ 0\right)$

$\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ -{\sqrt {3/2}},\ 0,\ 0\right)$

$\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ -2{\sqrt {2/5}},\ 0,\ 0,\ 0\right)$

$\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ -{\sqrt {5/3}},\ 0,\ 0,\ 0,\ 0\right)$

$\left({\sqrt {1/28}},\ -{\sqrt {12/7}},\ 0,\ 0,\ 0,\ 0,\ 0\right)$

$\left(-{\sqrt {7/4}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)$

More simply, the vertices of the 7-simplex can be positioned in 8-space as permutations of (0,0,0,0,0,0,0,1). This construction is based on facets of the 8-orthoplex.

Images

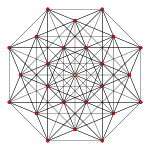
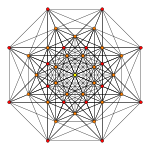
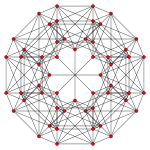
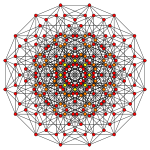
orthographic projections
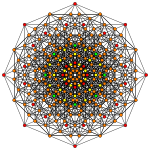
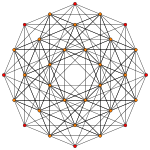
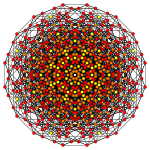
A_k Coxeter plane	A₇	A₆	A₅
Graph
Dihedral symmetry	[8]	[7]	[6]
A_k Coxeter plane	A₄	A₃	A₂
Graph
Dihedral symmetry	[5]	[4]	[3]

Related polytopes

This polytope is a facet in the uniform tessellation 3₃₁ with Coxeter-Dynkin diagram:

This polytope is one of 71 uniform 7-polytopes with A₇ symmetry.

t₀	t₁	t₂	t₃	t_0,1	t_0,2	t_1,2	t_0,3
t_1,3	t_2,3	t_0,4	t_1,4	t_2,4	t_0,5	t_1,5	t_0,6
t_0,1,2	t_0,1,3	t_0,2,3	t_1,2,3	t_0,1,4	t_0,2,4	t_1,2,4	t_0,3,4
t_1,3,4	t_2,3,4	t_0,1,5	t_0,2,5	t_1,2,5	t_0,3,5	t_1,3,5	t_0,4,5
t_0,1,6	t_0,2,6	t_0,3,6	t_0,1,2,3	t_0,1,2,4	t_0,1,3,4	t_0,2,3,4	t_1,2,3,4
t_0,1,2,5	t_0,1,3,5	t_0,2,3,5	t_1,2,3,5	t_0,1,4,5	t_0,2,4,5	t_1,2,4,5	t_0,3,4,5
t_0,1,2,6	t_0,1,3,6	t_0,2,3,6	t_0,1,4,6	t_0,2,4,6	t_0,1,5,6	t_0,1,2,3,4	t_0,1,2,3,5
t_0,1,2,4,5	t_0,1,3,4,5	t_0,2,3,4,5	t_1,2,3,4,5	t_0,1,2,3,6	t_0,1,2,4,6	t_0,1,3,4,6	t_0,2,3,4,6
t_0,1,2,5,6	t_0,1,3,5,6	t_0,1,2,3,4,5	t_0,1,2,3,4,6	t_0,1,2,3,5,6	t_0,1,2,4,5,6	t_{0,1,2,3,4,5,6}

Notes

↑ Richard Klitzing, 7D uniform polytopes (polyexa), x3o3o3o3o3o - oca

External links

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	A_n	BC_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.