7-cubic honeycomb
| 7-cubic honeycomb | |
|---|---|
| (no image) | |
| Type | Regular 7-space honeycomb |
| Family | Hypercube honeycomb |
| Schläfli symbol | {4,35,4} {4,34,31,1} {∞}7 |
| Coxeter-Dynkin diagrams | |
| 7-face type | {4,3,3,3,3,3} |
| 6-face type | {4,3,3,3,3} |
| 5-face type | {4,3,3,3} |
| 4-face type | {4,3,3} |
| Cell type | {4,3} |
| Face type | {4} |
| Face figure | {4,3} (octahedron) |
| Edge figure | 8 {4,3,3} (16-cell) |
| Vertex figure | 128 {4,35} (7-orthoplex) |
| Coxeter group | [4,35,4] |
| Dual | self-dual |
| Properties | vertex-transitive, edge-transitive, face-transitive, cell-transitive |
The 7-cubic honeycomb or hepteractic honeycomb is the only regular space-filling tessellation (or honeycomb) in Euclidean 7-space.
It is analogous to the square tiling of the plane and to the cubic honeycomb of 3-space.
There are many different Wythoff constructions of this honeycomb. The most symmetric form is regular, with Schläfli symbol {4,35,4}. Another form has two alternating 7-cube facets (like a checkerboard) with Schläfli symbol {4,34,31,1}. The lowest symmetry Wythoff construction has 128 types of facets around each vertex and a prismatic product Schläfli symbol {∞}7.
Related honeycombs
The [4,35,4], ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , Coxeter group generates 255 permutations of uniform tessellations, 135 with unique symmetry and 134 with unique geometry. The expanded 7-cubic honeycomb is geometrically identical to the 7-cubic honeycomb.
, Coxeter group generates 255 permutations of uniform tessellations, 135 with unique symmetry and 134 with unique geometry. The expanded 7-cubic honeycomb is geometrically identical to the 7-cubic honeycomb.
The 7-cubic honeycomb can be alternated into the 7-demicubic honeycomb, replacing the 7-cubes with 7-demicubes, and the alternated gaps are filled by 7-orthoplex facets.
Quadritruncated 7-cubic honeycomb
A quadritruncated 7-cubic honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , containins all tritruncated 7-orthoplex facets and is the Voronoi tessellation of the D7* lattice. Facets can be identically colored from a doubled
, containins all tritruncated 7-orthoplex facets and is the Voronoi tessellation of the D7* lattice. Facets can be identically colored from a doubled  ×2, [[4,35,4]] symmetry, alternately colored from
×2, [[4,35,4]] symmetry, alternately colored from  , [4,35,4] symmetry, three colors from
, [4,35,4] symmetry, three colors from 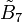 , [4,34,31,1] symmetry, and 4 colors from
, [4,34,31,1] symmetry, and 4 colors from 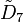 , [31,1,33,31,1] symmetry.
, [31,1,33,31,1] symmetry.
See also
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p. 296, Table II: Regular honeycombs
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
| Fundamental convex regular and uniform honeycombs in dimensions 2–11 | |||||
|---|---|---|---|---|---|
| Family |  |
 |
 |
 |
 / /  / / 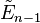 |
| Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| Uniform 5-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| Uniform 6-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| Uniform 7-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| Uniform 8-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| Uniform 9-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| Uniform n-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |