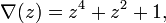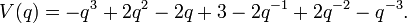6₃ knot

From Wikipedia, the free encyclopedia

6₃ knot

Arf invariant	1
Braid length	6
Braid no.	3
Bridge no.	2
Crosscap no.	3
Crossing no.	6
Hyperbolic volume	5.69302
Stick no.	8
Unknotting no.	1
Conway notation	[2112]
A-B notation	6₃
Dowker notation	4, 8, 10, 2, 12, 6
Last /Next	6₂ / 7₁
Other
alternating, hyperbolic, fibered, prime, fully amphichiral

In knot theory, the 6₃ knot is one of three prime knots with crossing number six, the others being the stevedore knot and the 6₂ knot.

Like the figure-eight knot, the 6₃ knot is amphichiral, meaning that it is indistinguishable from its own mirror image. It is also invertible, meaning that orienting the curve in either direction yields the same oriented knot.

The Alexander polynomial of the 6₃ knot is

$\Delta (t)=t^{2}-3t+5-3t^{{-1}}+t^{{-2}},\,$

the Conway polynomial is

$\nabla (z)=z^{4}+z^{2}+1,\,$

and the Jones polynomial is

$V(q)=-q^{3}+2q^{2}-2q+3-2q^{{-1}}+2q^{{-2}}-q^{{-3}}.\,$ ^[1]

The 6₃ knot is a hyperbolic knot, with its complement having a volume of approximately 5.69302.

References

↑ "6_3", The Knot Atlas.

v t e Knot theory (knots and links)

Hyperbolic	Figure-eight (4₁) Three-twist (5₂) Stevedore (6₁) 6₂ 6₃ Endless (7₄) Perko pair (10₁₆₁) (−2,3,7) pretzel (12n242) Borromean rings (63 2)

Satellite	Composite knots Granny Square

Torus	Unknot (0₁) Trefoil (3₁) Cinquefoil (5₁) Septafoil (7₁) Carrick mat (8₁₈) Unlink (02 1) Hopf (22 1) Solomon's (42 1) Whitehead (52 1) L10a140

Invariants	Alternating Arf invariant Bridge no. 2-bridge Brunnian Chirality Invertible Crosscap no. Crossing no. Finite type invariant Hyperbolic volume Genus Knot group Link group Linking no. Polynomial Alexander Bracket HOMFLY Jones Kauffman Pretzel Prime list Stick no. Tricolorability Unknotting no.

Notation & operations	Alexander–Briggs notation Conway notation Dowker notation Mutation Reidemeister move Skein relation

Other	Berge Braid theory Complement Double torus Fibered Framed Knot List of knots and links Ribbon Slice Sum Twist Wild

Category Commons

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.