2-bridge knot
From Wikipedia, the free encyclopedia
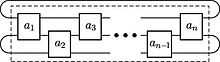
Schematic picture of a 2-bridge knot.
In the mathematical field of knot theory, a 2-bridge knot is a knot which can be isotoped so that the natural height function given by the z-coordinate has only two maxima and two minima as critical points.
Other names for 2-bridge knots are rational knots, 4-plats, and Viergeflechte. 2-bridge links are defined similarly as above, but each component will have one min and max. 2-bridge knots were classified by Herbert Seifert, using the fact that the 2-sheeted branched cover of the 3-sphere over the knot is a lens space.
The names rational knot and rational link were coined by John Conway who defined them as arising from numerator closures of rational tangles.
See also
Further reading
- Horst Schubert: Über Knoten mit zwei Brücken, Mathematische Zeitschrift 65:133–170 (1956).
- Louis H. Kauffman, Sofia Lambropoulou: On the classification of rational knots, L' Enseignement Mathématique, 49:357–410 (2003). preprint available at arxiv.org (Archived 2009-05-14).
- C. C. Adams, The Knot Book: An elementary introduction to the mathematical theory of knots. American Mathematical Society, Providence, RI, 2004. xiv+307 pp. ISBN 0-8218-3678-1
External links
| |||||||||||||||||||||||
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.