1-planar graph

A 1-planar drawing of the Heawood graph: six of the edges have a single crossing, and the remaining 15 edges are not crossed.

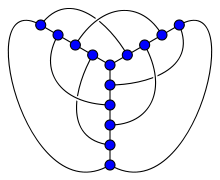
In topological graph theory, a 1-planar graph is a graph that can be drawn in the Euclidean plane in such a way that each edge has at most one crossing point, where it crosses a single additional edge.

Coloring

1-planar graphs were first studied by Ringel (1965), who showed that they can be colored with at most seven colors.^[1] Later, the precise number of colors needed to color these graphs, in the worst case, was shown to be six.^[2] The example of the complete graph K₆, which is 1-planar, shows that 1-planar graphs may sometimes require six colors. However, the proof that six colors are always enough is more complicated.

Coloring the vertices and faces of the triangular prism graph requires six colors

Ringel's motivation was in trying to solve a variation of total coloring for planar graphs, in which one simultaneously colors the vertices and faces of a planar graph in such a way that no two adjacent vertices have the same color, no two adjacent faces have the same color, and no vertex and face that are adjacent to each other have the same color. This can obviously be done using eight colors by applying the four color theorem to the given graph and its dual graph separately, using two disjoint sets of four colors. However, fewer colors may be obtained by forming an auxiliary graph that has a vertex for each vertex or face of the given planar graph, and in which two auxiliary graph vertices are adjacent whenever they correspond to adjacent features of the given planar graph. A vertex coloring of the auxiliary graph corresponds to a vertex-face coloring of the original planar graph. This auxiliary graph is 1-planar, from which it follows that Ringel's vertex-face coloring problem may also be solved with six colors.^[2] The graph K₆ cannot be formed as an auxiliary graph in this way, but nevertheless the vertex-face coloring problem also sometimes requires six colors; for instance, if the planar graph to be colored is a triangular prism, then its eleven vertices and faces require six colors, because no three of them may be given a single color.^[3]

Edge density

Every 1-planar graph with n vertices has at most 4n − 8 edges.^[4] More strongly, each 1-planar drawing has at most n − 2 crossings; removing one edge from each crossing pair of edges leaves a planar graph, which can have at most 3n − 6 edges, from which the 4n − 8 bound on the number of edges in the original 1-planar graph immediately follows.^[5]

The bound of 4n − 8 on the number of edges can be used to show that the complete graph K₇ on seven vertices is not 1-planar, because this graph has 21 edges and in this case 4n − 8 = 20 < 21.^[6] 1-planar graphs with exactly 4n − 8 edges may be formed from a planar graph, drawn in such a way that every face of the drawing is a quadrilateral, by adding two crossing diagonal edges within each quadrilateral. However, unlike planar graphs (for which all maximal planar graphs on a given vertex set have the same number of edges as each other), there exist maximal 1-planar graphs (graphs to which no additional edges can be added while preserving 1-planarity) that have significantly fewer than 4n − 8 edges.^[7]

The graphs that have straight 1-planar drawings (that is, drawings in which each edge is represented by a line segment, and in which each line segment is crossed by at most one other edge) have a slightly tighter bound of 4n − 9 on the maximum number of edges, achieved by infinitely many graphs.^[8]

Complete multipartite graphs

1-planar drawing of the cocktail party graph K_2,2,2,2

A complete classification of the 1-planar complete graphs, complete bipartite graphs, and more generally complete multipartite graphs is known. Every complete bipartite graph of the form K_2,n is 1-planar, as is every complete tripartite graph of the form K_1,1,n. Other than these infinite sets of examples, the only complete multipartite 1-planar graphs are K₆, K_1,1,1,6, K_1,1,2,3, K_2,2,2,2, K_1,1,1,2,2, and their subgraphs. The minimal non-1-planar complete multipartite graphs are K_3,7, K_4,5, K_1,3,4, K_2,3,3, and K_1,1,1,1,3. For instance, the complete bipartite graph K_3,6 is 1-planar because it is a subgraph of K_1,1,1,6, but K_3,7 is not 1-planar.^[6]

Computational complexity

It is NP-complete to test whether a given graph is 1-planar,^[9][10] and it remains NP-complete even for the graphs formed from planar graphs by adding a single edge^[11] and for graphs of bounded bandwidth.^[12] The problem is fixed-parameter tractable when parameterized by cyclomatic number or by tree-depth, so it may be solved in polynomial time when those parameters are bounded.^[12]

In contrast to Fáry's theorem for planar graphs, not every 1-planar graph may be drawn 1-planarly with straight line segments for its edges.^[13][14] However, testing whether a 1-planar drawing may be straightened in this way can be done in polynomial time.^[15]

1-planar graphs have bounded local treewidth, meaning that there is a (linear) function f such that the 1-planar graphs of diameter d have treewidth at most f(d); the same property holds more generally for the graphs that can be embedded onto a surface of bounded genus with a bounded number of crossings per edge. They also have separators, small sets of vertices the removal of which decomposes the graph into connected components whose size is a constant fraction of the size of the whole graph. Based on these properties, numerous algorithms for planar graphs, such as Baker's technique for designing approximation algorithms, can be extended to 1-planar graphs. For instance, this method leads to a polynomial-time approximation scheme for the maximum independent set of a 1-planar graph.^[16]

Generalizations and related concepts

1-planar graphs have been generalized to k-planar graphs, graphs for which each edge is crossed at most k times. The k-planar graphs with n vertices have at most O(n√k) edges.^[17] A shallow minor of a k-planar graph, with depth d, is itself a (2d + 1)k-planar graph, so the shallow minors of 1-planar graphs and of k-planar graphs are also sparse graphs.^[18]

Nonplanar graphs may also be parameterized by their crossing number, the minimum number of pairs of edges that cross in any drawing of the graph. A graph with crossing number k is necessarily k-planar, but not necessarily vice versa. For instance, the Heawood graph has crossing number 3, but it is not necessary for its three crossings to all occur on the same edge of the graph, so it is 1-planar, and can in fact be drawn in a way that simultaneously optimizes the total number of crossings and the crossings per edge.

References