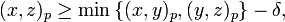Δ-hyperbolic space

From Wikipedia, the free encyclopedia

In mathematics, a δ-hyperbolic space is a geodesic metric space in which every geodesic triangle is δ-thin.

The δ-thin triangle condition

There are many equivalent definitions of "δ-thin". A simple definition is as follows: pick three points and draw geodesic lines between them to make a geodesic triangle. Then any point on any of the edges of the triangle is within a distance of δ from one of the other two sides.

For example, trees are 0-hyperbolic: a geodesic triangle in a tree is just a subtree, so any point on a geodesic triangle is actually on two edges. Normal Euclidean space is ∞-hyperbolic; i.e. not hyperbolic. Generally, the higher δ has to be, the less curved the space is.

The definition of δ-hyperbolic space is generally credited to Eliyahu Rips. There is also a definition of δ-hyperbolicity due to Mikhail Gromov. A geodesic metric space is said to be a Gromov δ-hyperbolic space if, for all p, x, y and z in X,

(x,z)_{{p}}\geq \min {\big \{}(x,y)_{{p}},(y,z)_{{p}}{\big \}}-\delta ,

where (x, y)p denotes the Gromov product of x and y at p. X is said to be simply Gromov hyperbolic if it is Gromov δ-hyperbolic for some δ ≥ 0.

See also

  • Negatively curved group

References


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.