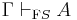Entailment
In logic, entailment is a relation between a set of sentences (e.g.,[1] meaningfully declarative sentences or truthbearers) and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent. S2 is called a tautological consequence of Γ; S1 is said to logically imply S2.
Two sentences are inconsistent if and only if they cannot both be true; they are logically inconsistent if and only if they are inconsistent as a result of their logical form.
Thus if
- Γ = {“Roses are red”, “Violets are blue”},
- S1 = “Roses are red and Violets are blue”
and
- S2 = “Violets are Blue”
then Γ entails S2, because
- “Roses are red and Violets are blue”
and
- “Violets are not blue”
are logically inconsistent. They are logically inconsistent because as a result of their logical form they cannot be both true, their logical forms being p and q and not-q.
On the other hand if
- Γ = {“John is a bachelor”},
- S1 = “John is a bachelor” and
- S2 = “John is a man”
then Γ does not entail S2 because
- S1, “John is a bachelor”
and
- (not)S2, “John is not a man”
are not logically inconsistent because they can both be true as a result of their logical form, their logical form being p and not-q.
Contents |
Logical form
Given Γ is a set of one or more declarative sentences.
Since
- Γ entails S2 if and only if S1 and not-S2 are logically inconsistent
and
- S1 and not-S2 are logically inconsistent if they are inconsistent as a result of their logical forms
it follows that
- Γ entails S2 if and only if S1 and not-S2 are inconsistent as a result of their logical forms.
It is therefore of the first importance to clarify the term logical form and explain how the logically relevant form(s)[2] of a sentence can be established.
The logical form of sentences can be revealed by means of a formal language enabling the following definition of entailment. Roughly, if S1 and S2 are interpretations of two sentences θ and ψ in a formal language of classical logic, then S1 entails S2 if and only if not (θ and not ψ) is true under all interpretations.
More precisely, if Γ is a set of one or more sentences and S1 is the conjunction of the elements of Γ and S2 is a sentence, Γ entails S2 if and only if not (S1 and not-S2) is a logical truth. S2 is called the 'logical consequent' of Γ. S1 is said to 'logically imply' S2.
Not (S1 and not-S2) is a logical truth if θ and Ψ are closed well-formed formulae (often denoted 'wff'), wffs (sentences) in a formal language L in classical logic, and I is an interpretation of L, and θ is true under I if and only if S1 and Ψ is true under I if and only if S2, and not (θ and not Ψ) is logically valid.
A closed wff Φ in L is 'logically valid' if and only if Φ is true under all interpretations of L. Hence
- Γ entails S2 iff not (θ and not Ψ) is logically valid.
Thus if Γ = {“Roses are red”, “Violets are blue”}, S1=“Roses are red and Violets are blue” and S2 = “Violets are Blue” then Γ entails S2 because not(S1 and not-S2), “It is not the case that roses are red and violets are blue and violets are not blue” is a logical truth.
Not(S1 and not-S2) is a logical truth because there are two closed wfs, P&Q and Q in a formal language L in classical logic and there is an interpretation I of L, and P&Q is true under I if and only if roses are red and violets are blue, and Q is true under I if and only if violets are blue, and ¬((P&Q)&¬Q) is logically valid. ¬((P&Q)&¬Q)) is logically valid because it is true under all interpretations of L (note that ¬ means not).
It will be noted that, on these definitions, if (i) S1 is inconsistent (self-contradictory) or (ii) not-S2 is inconsistent (self-contradictory) then (S1 and not-S2) is inconsistent (not consistent) and hence S1 entails S2.
Proof procedures, and relationship between entailment and deduction
It is of considerable interest to be able to prove that Γ entails S2 and hence that Γ/S2 is a valid argument. Ideally, entailment and deduction would be extensionally equivalent. However, this is not always the case. In such a case, it is useful to break the equivalence down into its two parts:
A deductive system S is complete for a language L if and only if 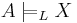 implies
implies 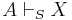 : that is, if all valid arguments are deducible (or provable), where
: that is, if all valid arguments are deducible (or provable), where 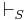 denotes the deducibility relation for the system S. NB
denotes the deducibility relation for the system S. NB 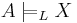 means that X is provable from A for a language L, and
means that X is provable from A for a language L, and 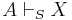 means that X is a semantic consequence of A for the system S.
means that X is a semantic consequence of A for the system S.
A deductive system S is sound for a language L if and only if 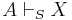 implies
implies 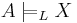 : that is, if no invalid arguments are provable.
: that is, if no invalid arguments are provable.
Many introductory textbooks (e.g. Mendelson's "Introduction to Mathematical Logic") that introduce first-order logic, include a complete and sound inference system for the first-order logic. In contrast, second-order logic — which allows quantification over predicates — does not have a complete and sound inference system with respect to a full Henkin (or standard) semantics.
Proof of entailment
Since
- Γ entails S2 iff not (θ and not Ψ) is logically valid
a proof that not (θ and not Ψ) is logically valid would be a proof that Γ entails S2.
It can be easily demonstrated, for example by means of a truth-table, that ¬((P & Q) & ¬Q) is a tautology and hence true under all interpretations and hence logically valid. Moreover, if T is a consistent theory in L and ¬(θ ∧ ¬Ψ) is a theorem in T (written ⊢T¬(θ ∧ ¬Ψ)) then ¬(θ ∧ ¬Ψ) is logically valid and, consequently, all interpretations of ¬(θ ∧ ¬Ψ) are logical truths, including not(S1 and not-S2). Hence Γ entails S2 if ⊢T¬(θ ∧ ¬Ψ) and T is consistent.
Relationship to other terms
Entailment is one of a number of inter-related terms of logical appraisal. Its relationship to other such terms includes the following see e.g. Strawson (1952)[3] Section 13, 'Entailment and Inconsistency', pp 19 et seq) where S1 and S2 are sentences, or S1 is the conjunction of all the sentences in some set of sentences Γ, S1 entails S2 if and only if:
- S1 and not-S2 are inconsistent (not consistent)
- (S1 and not-S2) is logically impossible
- Not(S1 and not-S2) is logically true
- Not(S1 and not-S2) is necessarily true
- (S1 and not-S2) is logically false
- S1 is a sufficient condition for S2
- S2 is a necessary condition for S1
- It would be self-contradictory to affirm S1 and deny S2
- An argument whose premise is S1 and conclusion is S2 is a valid argument
- If S1 and S2 are interpretations of two sentences θ and ψ in a formal language of classical logic (elementary logic), then S1 entails S2 if and only if not (θ and ¬ψ) is true in all interpretations.
Syntactic consequence
A formula A is a syntactic consequence[4][5][6][7] within some formal system FS of a set Г of formulas if there is a formal proof in FS of A from the set Г.
Syntactic consequence does not depend on any interpretation of the formal system.[8]
Semantic consequence
A formula A is a semantic consequence of a set of statements Г
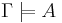 ,
,
if and only if no interpretation 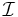 makes all members of Г true and A false.[9] Or, in other words, the set of the interpretations that make all members of Г true is a subset of the set of the interpretations that make A true.
makes all members of Г true and A false.[9] Or, in other words, the set of the interpretations that make all members of Г true is a subset of the set of the interpretations that make A true.
Entailment vs strict implication
The difference between strict implication and entailment is that entailment is a property of argument forms. The strict implication, on the other hand, is independent of argument forms.[10] For example, as demonstrated earlier, Γ = {"John is a bachelor."} does not entail "John is a man," because the argument forms of the sentences do not provide an entailment relation. On the other hand, the strict implication "John is a bachelor implies John is a man" is true; bachelors are men by definition, so there is no possible case in which John is a bachelor, but John is not a man.[11]
Entailment vs material implication
The difference between material implication and entailment is that they apply in different contexts. The first is a statement of logic, the second of metalogic. If p and q are two sentences then the difference between "p implies q" and "p is a proof of q" is that the first is a statement within formal logic, the second is a statement about it. Entailment is a concept of proof theory, [discuss] whereas material implication is the mechanics of a proof.
Limitations
Entailment is one form but not the only form of inference. Inductive reasoning is another. Scientific method involves inferences that are not solely entailment. Entailment does not encompass non-monotonic reasoning or defeasible reasoning. See also
Modal accounts
Modal accounts of logical consequence are variations on the following basic idea:
- Γ
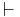 A just in case it is necessary that if all of the elements of Γ are true, then A is true.
A just in case it is necessary that if all of the elements of Γ are true, then A is true.
Alternatively (and, most would say, equivalently):
- Γ
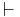 A just in case it is impossible for all of the elements of Γ to be true and A false.
A just in case it is impossible for all of the elements of Γ to be true and A false.
Such accounts are called "modal" because they appeal to the modal notions of necessity and (im)possibility. 'It is necessary that' is often cashed out as a universal quantifier over possible worlds, so that the accounts above translate as:
- Γ
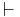 A just in case there is no possible world at which all of the elements of Γ are true and A is false (untrue).
A just in case there is no possible world at which all of the elements of Γ are true and A is false (untrue).
Consider the modal account in terms of the argument given as an example above:
- All frogs are green.
- Kermit is a frog.
- Therefore, Kermit is green.
The conclusion is a logical consequence of the premises because we can't imagine a possible world where (a) all frogs are green; (b) Kermit is a frog; and (c) Kermit is not green.
Modal-formal accounts
Modal-formal accounts of logical consequence combine the modal and formal accounts above, yielding variations on the following basic idea:
- Γ
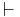 A just in case it is impossible for an argument with the same logical form as Γ/A to have true premises and a false conclusion.
A just in case it is impossible for an argument with the same logical form as Γ/A to have true premises and a false conclusion.
Most logicians would probably agree that logical consequence, as we intuitively understand it, has both a modal and a formal aspect, and that some version of the modal/formal account is therefore closest to being correct.
Warrant-based accounts
The accounts considered above are all "truth-preservational," in that they all assume that the characteristic feature of a good inference is that it never allows one to move from true premises to an untrue conclusion. As an alternative, some have proposed "warrant-preservational" accounts, according to which the characteristic feature of a good inference is that it never allows one to move from justifiably assertible premises to a conclusion that is not justifiably assertible. This is (roughly) the account favored by intuitionists such as Michael Dummett.
Non-monotonic logical consequence
The accounts discussed above all yield monotonic consequence relations, i.e. ones such that if A is a consequence of Γ, then A is a consequence of any superset of Γ. It is also possible to specify non-monotonic consequence relations to capture the idea that, e.g., 'Tweety can fly' is a logical consequence of
- {Birds can typically fly, Tweety is a bird}
but not of
- {Birds can typically fly, Tweety is a bird, Tweety is a penguin}.
For more on this, see belief revision#Non-monotonic inference relation.
Philosophical issues
- The literature is ambiguous regarding precisely what 'logical implication' means. Sometimes it is taken to be a pretheoretic notion capable of definition in several ways, usually involving modality and stated something like "A set of sentences logically implies a sentence A if and only if it is impossible that all the members of the set be true while A false". Other times it is taken as the definition given in the introduction to this article, perhaps as a replacement for the pretheoretic notion itself. This often occurs in the sciences and mathematics; that is, intuitive notions get replaced by more precise, rigorously defined ones. E.g., in mathematics, many now take 'computable' in the sense of 'effectively calculable' to be 'computable' in the sense of Turing, Church, Gödel, Herbrand, or Post.[12]
It is impossible to state rigorously the definition of 'logical implication' as it is understood pretheoretically, but many have taken the Tarskian model-theoretic account as a replacement for it. Some, e.g. Etchemendy 1990, have argued that they do not coincide, not even if they happen to be co-extensional (which Etchemendy believes they are not). This debate has received some recent attention. See "The Blackwell Guide to Philosophical Logic",[13] for a good introduction to it.
- It is often thought that a peculiar feature of logical implication is that a contradiction implies anything and that anything implies a validity. For example, 'Abraham Lincoln was president of the US' implies '2+2=4', and 'the white dot is black' implies 'the integer 25 is greater than the integer 30'. The peculiarity in these examples is oft-attributed to a lack of relevance between the two sentences. A formal notion of relevance has been characterized by relevant logic and applied to the notion of logical implication in the seminal work of Anderson & Belnap 1975. Another property they argue that implication should have is necessity. Thus A implies B only if it is necessary that A implies B. This feature of implication is lacking in the usual model-theoretic definition (i.e. the one given in the introduction).
- Some logicians draw a firm distinction between the conditional connective (the syntactic sign "
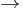 "), and the implication relation (the formal object denoted by the double arrow symbol "
"), and the implication relation (the formal object denoted by the double arrow symbol "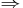 "). These logicians use the phrase not p or q for the conditional connective and the term implies for the implication relation. Some explain the difference by saying that the conditional is the contemplated relation while the implication is the asserted relation. In most fields of mathematics, it is treated as a variation in the usage of the single sign "
"). These logicians use the phrase not p or q for the conditional connective and the term implies for the implication relation. Some explain the difference by saying that the conditional is the contemplated relation while the implication is the asserted relation. In most fields of mathematics, it is treated as a variation in the usage of the single sign "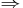 ", not requiring two separate signs. Not all of those who use the sign "
", not requiring two separate signs. Not all of those who use the sign "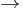 " for the conditional connective regard it as a sign that denotes any kind of object, but treat it as a so-called syncategorematic sign, that is, a sign with a purely syntactic function. For the sake of clarity and simplicity in the present introduction, it is convenient to use the two-sign notation, but allow the sign "
" for the conditional connective regard it as a sign that denotes any kind of object, but treat it as a so-called syncategorematic sign, that is, a sign with a purely syntactic function. For the sake of clarity and simplicity in the present introduction, it is convenient to use the two-sign notation, but allow the sign "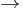 " to denote the boolean function that is associated with the truth table of the material conditional. These considerations result in the following scheme of notation.
" to denote the boolean function that is associated with the truth table of the material conditional. These considerations result in the following scheme of notation.
See also
Notes
- ^ It should be noted that entailment can be employed in sentences which are not necessarily truthbearers, but also to express contingencies in alethic modalities: imagined situations, evocative situations, or in situations involving necessity, duty, or the law.
- ^ We should not assume that a sentence has just one logical form. If T1 ="If Greeks are men and men are mortal then Greeks are men", we could say that the logical form of T1 is "IF P and Q THEN P", and thus the logical form of ."Greeks are men" is "P". If T2 is ="If Greeks are men and men are mortal then Greeks are mortal", we could say that the logical from of T2 is "If all A is B and all B is C then all A is C", and thus the logical form of "Greeks are men" is "All A is B". Hence we cannot say that THE logical form of "Greeks are men" is "P" nor "All A is B".
- ^ Strawson, P.F. (1952). Introduction to Logical Theory. Methuen.
- ^ Dummett, Michael (1993) Frege: philosophy of language Harvard University Press, p.82ff
- ^ Lear, Jonathan (1986) Aristotle and Logical Theory Cambridge University Press, 136p.
- ^ Creath, Richard, and Friedman, Michael (2007) The Cambridge companion to Carnap Cambridge University Press, 371p.
- ^ FOLDOC: "syntactic consequence"
- ^ Hunter, Geoffrey, Metalogic: An Introduction to the Metatheory of Standard First-Order Logic, University of California Pres, 1971, p. 75.
- ^ The Cambridge Dictionary of Philosophy
- ^ Larson et al. 2007, pp. 79-80
- ^ Larson et al. 2007, pp. 79-80
- ^ See for example Davis 1965
- ^ Goble 2001 Chapter 6
Resources
- Anderson, A.R.; Belnap, N.D., Jr. (1975), Entailment, 1, Princeton, NJ: Princeton.
- Barwise, Jon; Etchemendy, John (2008), Language, Proof and Logic, Stanford: CSLI Publications.
- Brown, Frank Markham (2003), Boolean Reasoning: The Logic of Boolean Equations 1st edition, Kluwer Academic Publishers, Norwell, MA. 2nd edition, Dover Publications, Mineola, NY, 2003.
- Davis, Martin, (editor) (1965), The Undecidable, Basic Papers on Undecidable Propositions, Unsolvable Problems And Computable Functions, New York: Raven Press. Papers include those by Gödel, Church, Rosser, Kleene, and Post.
- Dummett, Michael (1991), The Logical Basis of Metaphysics, Harvard University Press.
- Edgington, Dorothy (2001), Conditionals, Blackwell in Lou Goble (ed.), The Blackwell Guide to Philosophical Logic.
- Edgington, Dorothy (2006), Conditionals, http://plato.stanford.edu/entries/conditionals in Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy.
- Etchemendy, John (1990), The Concept of Logical Consequence, Harvard University Press.
- Goble, Lou, ed. (2001), The Blackwell Guide to Philosophical Logic, Blackwell.
- Hanson, William H (1997), "The concept of logical consequence", The Philosophical Review 106 365–409.
- Hendricks, Vincent F. (2005), Thought 2 Talk: A Crash Course in Reflection and Expression, New York: Automatic Press / VIP, ISBN 87-991013-7-8
- Larson, Ron; Boswell, Laurie; Kanold, Timothy D.; Stiff, Lee (2007), Geometry, McDougal Littell.
- Planchette, P. A. (2001), Logical Consequence in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.
- Quine, W.V. (1982), Methods of Logic, Cambridge, MA: Harvard University Press (1st ed. 1950), (2nd ed. 1959), (3rd ed. 1972), (4th edition, 1982).
- Shapiro, Stewart (2002), Necessity, meaning, and rationality: the notion of logical consequence in D. Jacquette, ed., A Companion to Philosophical Logic. Blackwell.
- Tarski, Alfred (1936), On the concept of logical consequence Reprinted in Tarski, A., 1983. Logic, Semantics, Metamathematics, 2nd ed. Oxford University Press. Originally published in Polish and German.
- A paper on 'implication' from math.niu.edu, Implication
- A definition of 'implicant' AllWords
External links
|
|
|||||||||||||||||||