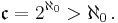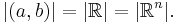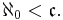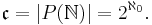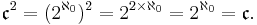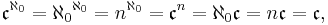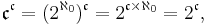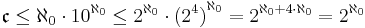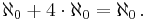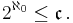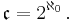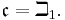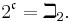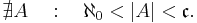Cardinality of the continuum

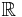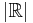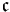In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers $\mathbb R$ , sometimes called the continuum. It is an infinite cardinal number and is denoted by $|\mathbb R|$ or $\mathfrak c$ (a lowercase fraktur script c).

The real numbers 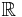$\mathbb R$ are more numerous than the natural numbers 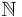$\mathbb N$ . Moreover, 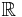$\mathbb R$ has the same number of elements as the power set of 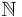$\mathbb N$ . Symbolically, if the cardinality of 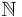$\mathbb N$ is denoted as 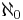$\aleph_0$ , the cardinality of the continuum is

$\mathfrak c = 2^{\aleph_0} > \aleph_0 \,.$

This was proven by Georg Cantor in his 1874 uncountability proof, part of his groundbreaking study of different infinities, and later more simply in his diagonal argument. Cantor defined cardinality in terms of bijective functions: two sets have the same cardinality if and only if there exists a bijective function between them.

Between any two real numbers a < b, no matter how close they are to each other, there are always infinitely many other real numbers, and Cantor showed that they are as many as those contained in the whole set of real numbers. In other words, the open interval (a,b) is equinumerous with 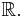$\mathbb R.$ This is also true for several other infinite sets, such as any n-dimensional Euclidean space 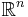$\mathbb R^n$ (see Space filling curve). That is,

$|(a,b)| = |\mathbb R| = |\mathbb R^n|.$

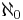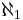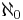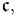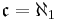The smallest infinite cardinal number is $\aleph_0$ (aleph-naught). The second smallest is $\aleph_1$ (aleph-one). The continuum hypothesis, which asserts that there are no sets whose cardinality is strictly between $\aleph_0$ and $\mathfrak c,$ implies that $\mathfrak c = \aleph_1$ .

1 Properties
2 Beth numbers
3 The continuum hypothesis
4 Sets with cardinality of the continuum
5 Sets with greater cardinality
6 References

Properties

Uncountability

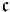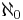Georg Cantor introduced the concept of cardinality to compare the sizes of infinite sets. He famously showed that the set of real numbers is uncountably infinite; i.e. ${\mathfrak c}$ is strictly greater than the cardinality of the natural numbers, $\aleph_0$ :

$\aleph_0 < \mathfrak c.$

In other words, there are strictly more real numbers than there are integers. Cantor proved this statement in several different ways. See Cantor's first uncountability proof and Cantor's diagonal argument.

Cardinal equalities

A variation on Cantor's diagonal argument can be used to prove Cantor's theorem which states that the cardinality of any set is strictly less than that of its power set, i.e. |A| < 2^|A|, and so the power set P(N) of the natural numbers N is uncountable. In fact, it can be shown that the cardinality of P(N) is equal to 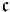${\mathfrak c}$ :

Define a map f : R → P(Q) from the reals to the power set of the rationals by sending each real number x to the set 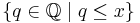$\{q \in \mathbb{Q} \mid q \le x\}$ of all rationals less than or equal to x (with the reals viewed as Dedekind cuts, this is nothing other than the inclusion map in the set of sets of rationals). This map is injective since the rationals are dense in R. 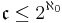Since the rationals are countable we have that $\mathfrak c \le 2^{\aleph_0}$ .
Let {0,2}^N be the set of infinite sequences with values in set {0,2}. This set clearly has cardinality 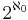$2^{\aleph_0}$ (the natural bijection between the set of binary sequences and P(N) is given by the indicator function). Now associate to each such sequence (a_i) the unique real number in the interval [0,1] with the ternary-expansion given by the digits (a_i), i.e. the i-th digit after the decimal point is a_i. The image of this map is called the Cantor set. It is not hard to see that this map is injective, for by avoiding points with the digit 1 in their ternary expansion we avoid conflicts created by the fact that the ternary-expansion of a real number is not unique. 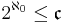We then have that $2^{\aleph_0} \le \mathfrak c$ .

By the Cantor–Bernstein–Schroeder theorem we conclude that

$\mathfrak c = |P(\mathbb{N})| = 2^{\aleph_0}.$

(A different proof of 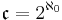$\mathfrak c = 2^{\aleph_0}$ is given in Cantor's diagonal argument. This proof constructs a bijection from {0,1}^N to R.)

The cardinal equality 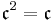$\mathfrak{c}^2 = \mathfrak{c}$ can be demonstrated using cardinal arithmetic:

$\mathfrak{c}^2 = (2^{\aleph_0})^2 = 2^{2\times{\aleph_0}} = 2^{\aleph_0} = \mathfrak{c}.$

This argument is a condensed version of the notion of interleaving two binary sequences: let 0.a₀a₁a₂... be the binary expansion of x and let 0.b₀b₁b₂... be the binary expansion of y. Then z = 0.a₀b₀a₁b₁a₂b₂..., the interleaving of the binary expansions, is a well-defined function when x and y have unique binary expansions. Only countably many reals have non-unique binary expansions.

By using the rules of cardinal arithmetic one can also show that

$\mathfrak c^{\aleph_0} = {\aleph_0}^{\aleph_0} = n^{\aleph_0} = \mathfrak c^n = \aleph_0 \mathfrak c = n \mathfrak c = \mathfrak c,$

where n is any finite cardinal ≥ 2, and

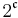$\mathfrak c ^{\mathfrak c} = (2^{\aleph_0})^{\mathfrak c} = 2^{\mathfrak c\times\aleph_0} = 2^{\mathfrak c},$

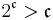where $2 ^{\mathfrak c}$ is the cardinality of the power set of R, and $2 ^{\mathfrak c} > \mathfrak c$ .

Alternative explanation for 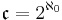${\mathfrak c} = 2^{\aleph_0}$

Every real number has an infinite decimal expansion. For example,

1/2 = 0.50000...

1/3 = 0.33333...

$\pi$ = 3.14159....

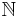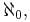(This is true even when the expansion repeats as in the first two examples.) In any given case, the number of digits is countable since they can be put into a one-to-one correspondence with the set of natural numbers $\mathbb{N}$ . This fact makes it sensible to talk about (for example) the first, the one-hundredth, or the millionth digit of $\pi$ . Since the natural numbers have cardinality $\aleph_0,$ each real number has 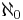$\aleph_0$ digits in its expansion.

Since each real number can be broken into an integer part and a decimal fraction, we get

${\mathfrak c} \leq \aleph_0 \cdot 10^{\aleph_0} \leq 2^{\aleph_0} \cdot {(2^4)}^{\aleph_0} = 2^{\aleph_0 %2B 4 \cdot \aleph_0} = 2^{\aleph_0}$

since

$\aleph_0 %2B 4 \cdot \aleph_0 = \aleph_0 \,.$

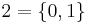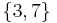On the other hand, if we map $2 = \{0, 1\}$ to $\{3, 7\}$ and consider that decimal fractions containing only 3 or 7 are only a part of the real numbers, then we get

$2^{\aleph_0} \leq {\mathfrak c} \,.$

and thus

${\mathfrak c} = 2^{\aleph_0} \,.$

Beth numbers

Main article: Beth number

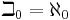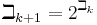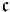The sequence of beth numbers is defined by setting $\beth_0 = \aleph_0$ and $\beth_{k%2B1} = 2^{\beth_k}$ . So ${\mathfrak c}$ is the second beth number, beth-one:

$\mathfrak c = \beth_1.$

The third beth number, beth-two, is the cardinality of the power set of R (i.e. the set of all subsets of the real line):

$2^\mathfrak c = \beth_2.$

The continuum hypothesis

Main article: Continuum hypothesis

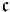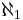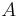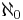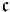
The famous continuum hypothesis asserts that ${\mathfrak c}$ is also the second aleph number $\aleph_1$ . In other words, the continuum hypothesis states that there is no set $A\,$ whose cardinality lies strictly between $\aleph_0$ and ${\mathfrak c}$

$\nexists A \quad:\quad \aleph_0 < |A| < \mathfrak c.$

This statement is now known to be independent of the axioms of Zermelo–Fraenkel set theory with the axiom of choice (ZFC). That is, both the hypothesis and its negation are consistent with these axioms. In fact, for every nonzero natural number n, the equality 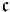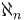${\mathfrak c}$ = $\aleph_n$ is independent of ZFC. 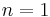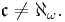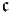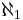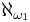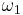(The case $n=1$ is the continuum hypothesis.) The same is true for most other alephs, although in some cases equality can be ruled out by König's theorem on the grounds of cofinality, e.g., $\mathfrak{c}\neq\aleph_\omega.$ In particular, $\mathfrak{c}$ could be either $\aleph_1$ or $\aleph_{\omega_1}$ , where $\omega_1$ is the first uncountable ordinal, so it could be either a successor cardinal or a limit cardinal, and either a regular cardinal or a singular cardinal.

Sets with cardinality of the continuum

A great many sets studied in mathematics have cardinality equal to 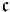${\mathfrak c}$ . Some common examples are the following:

the real numbers $\mathbb{R}$
any (nondegenerate) closed or open interval in $\mathbb{R}$ (such as the unit interval [0,1])
the irrational numbers
the transcendental numbers
the Cantor set
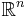
Euclidean space $\mathbb{R}^n$
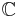
the complex numbers $\mathbb{C}$
the power set of the natural numbers 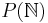$P(\mathbb{N})$ (the set of all subsets of the natural numbers)
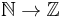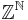the set of sequences of integers (i.e. all functions $\mathbb{N} \rightarrow \mathbb{Z}$ , often denoted $\mathbb{Z}^\mathbb{N}$ )
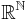
the set of sequences of real numbers, $\mathbb{R}^\mathbb{N}$
the set of all continuous functions from $\mathbb{R}$ to $\mathbb{R}$
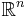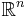the Euclidean topology on $\mathbb{R}^n$ (i.e. the set of all open sets in $\mathbb{R}^n$ )
the Borel σ-algebra on $\mathbb{R}$ (i.e. the set of all Borel sets in $\mathbb{R}$ ).

Sets with greater cardinality

Sets with cardinality greater than 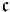${\mathfrak c}$ include:

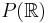the set of all subsets of $\mathbb{R}$ (i.e., power set $P(\mathbb{R})$ )
the set 2^R of indicator functions defined on subsets of the reals (the set 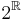$2^{\mathbb{R}}$ is isomorphic to 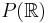$P(\mathbb{R})$ – the indicator function chooses elements of each subset to include)
the set 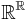$\mathbb{R}^\mathbb{R}$ of all functions from $\mathbb{R}$ to $\mathbb{R}$
the Lebesgue σ-algebra of $\mathbb{R}$ , i.e., the set of all Lebesgue measurable sets in $\mathbb{R}$ .
the Stone–Čech compactifications of 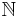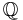$\mathbb{N}$ , $\mathbb{Q}$ and $\mathbb{R}$ .

They all have cardinality 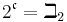$2^\mathfrak c = \beth_2$ (Beth two).

References

Paul Halmos, Naive set theory. Princeton, NJ: D. Van Nostrand Company, 1960. Reprinted by Springer-Verlag, New York, 1974. ISBN 0-387-90092-6 (Springer-Verlag edition).
Jech, Thomas, 2003. Set Theory: The Third Millennium Edition, Revised and Expanded. Springer. ISBN 3-540-44085-2.
Kunen, Kenneth, 1980. Set Theory: An Introduction to Independence Proofs. Elsevier. ISBN 0-444-86839-9.

This article incorporates material from cardinality of the continuum on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.