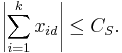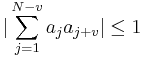±1-sequence

In mathematics, a ±1–sequence, (x₁, x₂, x₃, ...), is a sequence where each x_i is one of {1, −1}.

Such sequences are commonly studied in discrepancy theory.

1 Erdős discrepancy problem
2 Barker Codes
3 See also
4 Notes
5 References
6 External links

Erdős discrepancy problem

Let S=(x₁, x₂, x₃,...) be a ±1–sequence, where x_j denotes the j^th term. The Erdős discrepancy problem asks whether there exists a sequence S and an integer C_S, such that for any two positive integers d and k,

$\left| \sum_{i=1}^k x_{id} \right| \leq C_S.$

As of October 2010^[update], this problem is currently being studied by the Polymath project.

Barker Codes

Main article: Barker code

A Barker code is a sequence of N values of +1 and −1,

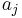$a_j$ for j = 1, 2, …, N

such that

$|\sum_{j=1}^{N-v} a_j a_{j%2Bv}| \le 1\,$

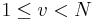for all $1 \le v < N$ .^[1]

Barker codes of length 11 and 13 are used in direct-sequence spread spectrum and pulse compression radar systems because of their low autocorrelation properties.

Notes

^ Barker, R. H. (1953). "Group Synchronizing of Binary Digital Sequences". Communication Theory. London: Butterworth. pp. 273–287.

References

Chazelle, Bernard. The Discrepancy Method: Randomness and Complexity. Cambridge University Press. ISBN 0-521-77093-9.

External links

The Erdős discrepancy problem – Polymath Project