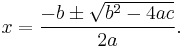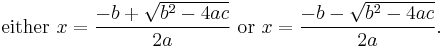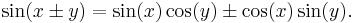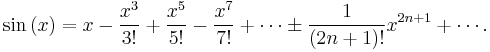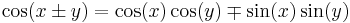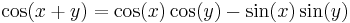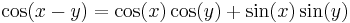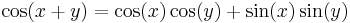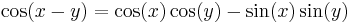Plus-minus sign

The plus-minus sign (±) is a mathematical symbol commonly used either

to indicate the precision of an approximation, or
to indicate a value that can be of either sign.

The sign is normally pronounced "plus or minus". In experimental sciences, the sign commonly indicates the confidence interval or error in a measurement, often the standard deviation or standard error. The sign may also represent an inclusive range of values that a reading might have. In mathematics, it may indicate two possible values: one positive, and one negative.

1 Precision indication
2 Shorthand
3 Minus-plus sign
4 Other uses
5 Encodings
6 Similar characters
7 See also

Precision indication

The use of ± for an approximation is most commonly encountered in presenting the numerical value of a quantity together with its tolerance or its statistical margin of error. For example, "5.7±0.2" denotes a quantity that is specified or estimated to be within 0.2 units of 5.7; it may be anywhere in the range from 5.7 − 0.2 (i.e., 5.5) to 5.7 + 0.2 (5.9). In scientific usage it sometimes refers to a probability of being within the stated interval, usually corresponding to either 1 or 2 standard deviations (a probability of 68.3% or 95.4% in a Normal distribution).

A percentage may also be used to indicate the error margin. For example, 230 ± 10% V refers to a voltage within 10% of either side of 230 V (207 V to 253 V). Separate values for the upper and lower bounds may also be used. For example, to indicate that a value is most likely 5.7 but may be as high as 5.9 or as low as 5.6, one could write 5.7+0.2
−0.1.

Shorthand

In mathematical equations, the use of ± may be found as shorthand, to present two equations in one formula: + or −, represented with ±.

For example, given the equation x² = 1, one may give the solution as x = ±1, such that both x = +1 and x = −1 are valid solutions.

More generally we have the quadratic formula:

If ax² + bx + c = 0 then

$\displaystyle x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}.$

Written out in full, this states that there are two solutions to the equation, i.e. that

$\text{either } x = \frac{-b %2B \sqrt {b^2-4ac}}{2a} \text{ or } x = \frac{-b - \sqrt {b^2-4ac}}{2a}.$

Another example is found in the trigonometric identity

$\sin(x \pm y) = \sin(x) \cos(y) \pm \cos(x) \sin(y).\,$

This stands for two identities: one with "+" on both sides of the equation, and one with "−" on both sides.

A somewhat different use is found in this presentation of the formula for the Taylor series of the sine function:

$\sin\left( x \right) = x - \frac{x^3}{3!} %2B \frac{x^5}{5!} - \frac{x^7}{7!} %2B \cdots \pm \frac{1}{(2n%2B1)!} x^{2n%2B1} %2B \cdots.$

This mild abuse of notation is intended to indicate that the signs of the terms alternate, where (starting the count at 0) the terms with an even index n are added while those with an odd index are subtracted. A more rigorous presentation would use the expression (−1)ⁿ, which gives +1 when n is even and −1 when n is odd.

Minus-plus sign

There is another character, the minus-plus sign (∓). It is generally used in conjunction with the "±" sign, in such expressions as "x ± y ∓ z", which can be interpreted as meaning "x + y − z" or/and "x − y + z", but not "x + y + z" nor "x − y − z". The upper "−" in "∓" is considered to be associated to the "+" of "±" (and similarly for the two lower symbols) even though there is no visual indication of the dependency. The original expression can be rewritten as "x ± (y − z)" to avoid confusion, but cases such as the trigonometric identity

$\cos(x \pm y) = \cos(x) \cos(y) \mp \sin(x) \sin(y)$

are most neatly written using the "∓" sign. The trigonometric equation above thus represents the two equations:

$\cos(x %2B y) = \cos(x)\cos(y) - \sin(x) \sin(y)\,$

$\cos(x - y) = \cos(x)\cos(y) %2B \sin(x) \sin(y)\,$

but never

$\cos(x %2B y) = \cos(x)\cos(y) %2B \sin(x) \sin(y)\,$

$\cos(x - y) = \cos(x)\cos(y) - \sin(x) \sin(y)\,$

because the signs are exclusively alternating.

Other uses

± and ∓ are used in chess notation to denote an advantage for white and black respectively.

Encodings

In ISO 8859-1, -7, -8, -9, -13, -15, and -16, the plus-minus symbol is given by the code 0xB1_hex Since the first 256 code points of Unicode are identical to the contents of ISO-8859-1 this symbol is also at Unicode code point U+00B1.
The symbol also has a HTML entity representation of ±.
On Windows systems, it may be entered by means of Alt codes, by holding the ALT key while typing the numbers 0177 on the numeric keypad.
On Unix-like systems, it can be entered by typing the sequence compose + -.
On Macintosh systems, it may be entered by pressing option shift = (on the non-numeric keypad).
The rarer minus-plus sign (∓) is not generally found in legacy encodings and does not have a named HTML entity but is available in Unicode with codepoint U+2213 and so can be used in HTML using ∓ or ∓.
In TeX 'plus-or-minus' and 'minus-or-plus' symbols are denoted \pm and \mp, respectively.
These characters are also seen written as a (rather untidy) underlined or overlined + symbol. ( + or + ).

Similar characters

The plus-minus sign resembles the Chinese character 士, whereas the minus-plus sign resembles 干.