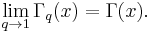q-gamma function
In q-analog theory, the q-gamma function, or basic gamma function, is a generalization of the ordinary Gamma function closely related to the double gamma function. It was introduced by Jackson (1905). It is given by
where 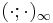 is the infinite q-Pochhammer symbol. It satisfies the functional equation
is the infinite q-Pochhammer symbol. It satisfies the functional equation
For non-negative integers n,
where ![[\cdot]_q!](/2012-wikipedia_en_all_nopic_01_2012/I/9e97878593a422f3f205c7db41ee0fcf.png) is the q-factorial function. Alternatively, this can be taken as an extension of the q-factorial function to the real number system.
is the q-factorial function. Alternatively, this can be taken as an extension of the q-factorial function to the real number system.
The relation to the ordinary gamma function is made explicit in the limit
References
- Jackson, F. H. (1905), "The Basic Gamma-Function and the Elliptic Functions", Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character (The Royal Society) 76 (508): 127–144, ISSN 0950-1207, JSTOR 92601
- Gasper, George; Rahman, Mizan (2004), Basic hypergeometric series, Encyclopedia of Mathematics and its Applications, 96 (2nd ed.), Cambridge University Press, ISBN 978-0-521-83357-8, MR2128719
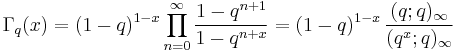
![\Gamma_q(x%2B1) = \frac{1-q^{x}}{1-q}\Gamma_q(x)=[x]_q\Gamma_q(x)](/2012-wikipedia_en_all_nopic_01_2012/I/9310a31ab39ca066c83aa9259b29864f.png)
![\Gamma_q(n)=[n-1]_q!](/2012-wikipedia_en_all_nopic_01_2012/I/6da31139789e0da2380d0cafddd86266.png)