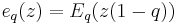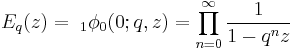q-exponential
Not to be confused with the Tsallis q-exponential.
In combinatorial mathematics, the q-exponential is a q-analog of the exponential function.
Definition
The q-exponential 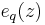 is defined as
is defined as
where ![[n]_q!](/2012-wikipedia_en_all_nopic_01_2012/I/4068da6f34e0edc79705024cdc294e3d.png) is the q-factorial and
is the q-factorial and
is the q-Pochhammer symbol. That this is the q-analog of the exponential follows from the property
where the derivative on the left is the q-derivative. The above is easily verified by considering the q-derivative of the monomial
Here, ![[n]_q](/2012-wikipedia_en_all_nopic_01_2012/I/94afffce1a5ca1d85aca3a7ed181aa2f.png) is the q-bracket.
is the q-bracket.
Properties
For real 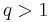 , the function
, the function 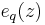 is an entire function of z. For
is an entire function of z. For  ,
, 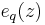 is regular in the disk
is regular in the disk 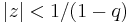 .
.
Relations
For  , a function that is closely related is
, a function that is closely related is
Here, 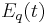 is a special case of the basic hypergeometric series:
is a special case of the basic hypergeometric series:
![e_q(z)=
\sum_{n=0}^\infty \frac{z^n}{[n]_q!} =
\sum_{n=0}^\infty \frac{z^n (1-q)^n}{(q;q)_n} =
\sum_{n=0}^\infty z^n\frac{(1-q)^n}{(1-q^n)(1-q^{n-1}) \cdots (1-q)}](/2012-wikipedia_en_all_nopic_01_2012/I/e15c462a0b44434270ccf2f394fb799d.png)
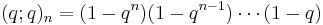
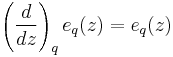
![\left(\frac{d}{dz}\right)_q z^n = z^{n-1} \frac{1-q^n}{1-q}
=[n]_q z^{n-1}.](/2012-wikipedia_en_all_nopic_01_2012/I/23a1aaaf482ca1996693456a7858adec.png)