q-derivative
In mathematics, in the area of combinatorics, the q-derivative, or Jackson derivative, is a q-analog of the ordinary derivative, introduced by Frank Hilton Jackson. It is the inverse of Jackson's q-integration
Contents |
Definition
The q-derivative of a function f(x) is defined as
It is also often written as 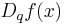 . The q-derivative is also known as the Jackson derivative. It is a linear operator
. The q-derivative is also known as the Jackson derivative. It is a linear operator
It has product rule analogous to the ordinary derivative product rule which has two equivalent forms
Similarly it satisfies a quotient rule
There is also a rule similar to the chain rule for ordinary derivatives. Let 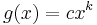 . Then
. Then
Relationship to ordinary derivatives
Q-differentiation resembles ordinary differentiation, with curious differences. For example, the q-derivative of the monomial is:
where ![[n]_q](/2012-wikipedia_en_all_nopic_01_2012/I/94afffce1a5ca1d85aca3a7ed181aa2f.png) is the q-bracket of n. Note that
is the q-bracket of n. Note that ![\lim_{q\to 1}[n]_q = n](/2012-wikipedia_en_all_nopic_01_2012/I/a16ea7eae0dca1369c416d8a9e3ee329.png) so the ordinary derivative is regained in this limit.
so the ordinary derivative is regained in this limit.
The n-th q-derivative of a function may be given as:
provided that the ordinary n-th derivative of f exists at x=0. Here, 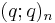 is the q-Pochhammer symbol, and
is the q-Pochhammer symbol, and ![[n]_q!](/2012-wikipedia_en_all_nopic_01_2012/I/4068da6f34e0edc79705024cdc294e3d.png) is the q-factorial. If
is the q-factorial. If  is analytic we can apply the Taylor formula to the definition of
is analytic we can apply the Taylor formula to the definition of 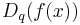 to get
to get
A q-analog of the Taylor expansion of a function about zero follows:
See also
- Derivative (generalizations)
- Jackson integral
- Q-exponential
- Q-difference polynomials
- Quantum calculus
- Tsallis entropy
References
- Victor Kac, Pokman Cheung, Quantum Calculus, Universitext, Springer-Verlag, 2002. ISBN 0-387-95341-8
Further reading
- J. Koekoek, R. Koekoek, A note on the q-derivative operator, (1999) ArXiv math/9908140
- Thomas Ernst, The History of q-Calculus and a new method,(2001),
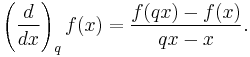
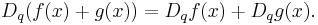
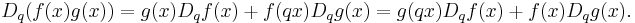
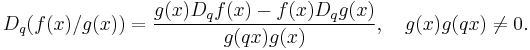
![\left(\frac{d}{dz}\right)_q z^n = \frac{1-q^n}{1-q} z^{n-1} =
[n]_q z^{n-1}](/2012-wikipedia_en_all_nopic_01_2012/I/9947b7d31a33f0f4adad24722f9ac84d.png)
![(D^n_q f)(0)=
\frac{f^{(n)}(0)}{n!} \frac{(q;q)_n}{(1-q)^n}=
\frac{f^{(n)}(0)}{n!} [n]_q!](/2012-wikipedia_en_all_nopic_01_2012/I/986d4f5262809d95412717ade3e57f4a.png)
![f(z)=\sum_{n=0}^\infty f^{(n)}(0)\,\frac{z^n}{n!} = \sum_{n=0}^\infty (D^n_q f)(0)\,\frac{z^n}{[n]_q!}](/2012-wikipedia_en_all_nopic_01_2012/I/5455d15e6e9fd9705893b8af3a6de2f1.png)