p-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element. Such groups are also called p-primary or simply primary.
A finite group is a p-group if and only if its order (the number of its elements) is a power of p. The remainder of this article deals with finite p-groups. For an example of an infinite abelian p-group, see Prüfer group, and for an example of an infinite simple p-group, see Tarski monster group.
Contents[hide] |
Properties
Quite a lot is known about the structure of finite p-groups.
Non-trivial center
One of the first standard results using the class equation is that the center of a non-trivial finite p-group cannot be the trivial subgroup (proof).
This forms the basis for many inductive methods in p-groups.
For instance, the normalizer N of a proper subgroup H of a finite p-group G properly contains H, because for any counterexample with H=N, the center Z is contained in N, and so also in H, but then there is a smaller example H/Z whose normalizer in G/Z is N/Z=H/Z, creating an infinite descent. As a corollary, every finite p-group is nilpotent.
In another direction, every normal subgroup of a finite p-group intersects the center nontrivially. In particular, every minimal normal subgroup of a finite p-group is of order p and contained in the center. Indeed, the socle of a finite p-group is the subgroup of the center consisting of the central elements of order p.
If G is a p-group, then so is G/Z, and so it too has a nontrivial center. The preimage in G of the center of G/Z is called the second center and these groups begin the upper central series. Generalizing the earlier comments about the socle, a finite p-group with order pn contains normal subgroups of order pi with 0 ≤ i ≤ n, and any normal subgroup of order pi is contained in the ith center Zi. If a normal subgroup is not contained in Zi, then its intersection with Zi+1 has size at least pi+1.
Automorphisms
The automorphism groups of p-groups are well studied. Just as every finite p-group has a nontrivial center so that the inner automorphism group is a proper quotient of the group, every finite p-group has a nontrivial outer automorphism group. Every automorphism of G induces an automorphism on G/Φ(G), where Φ(G) is the Frattini subgroup of G. The quotient G/Φ(G) is an elementary abelian group and its automorphism group is a general linear group, so very well understood. The map from the automorphism group of G into this general linear group has been studied by Burnside, who showed that the kernel of this map is a p-group.
Examples
p-groups of the same order are not necessarily isomorphic; for example, the cyclic group C4 and the Klein group V4 are both 2-groups of order 4, but they are not isomorphic.
Nor need a p-group be abelian; the dihedral group Dih4 of order 8 is a non-abelian 2-group. However, every group of order p2 is abelian.[note 1]
The dihedral groups are both very similar to and very dissimilar from the quaternion groups and the semidihedral groups. Together the dihedral, semidihedral, and quaternion groups form the 2-groups of maximal class, that is those groups of order 2n+1 and nilpotency class n.
Iterated wreath products
The iterated wreath products of cyclic groups of order p are very important examples of p-groups. Denote the cyclic group of order p as W(1), and the wreath product of W(n) with W(1) as W(n+1). Then W(n) is the Sylow p-subgroup of the symmetric group Sym(pn). Maximal p-subgroups of the general linear group GL(n,Q) are direct products of various W(n). It has order pk where k=(pn−1)/(p−1). It has nilpotency class pn−1, and its lower central series, upper central series, lower exponent-p central series, and upper exponent-p central series are equal. It is generated by its elements of order p, but its exponent is pn. The second such group, W(2), is also a p-group of maximal class, since it has order pp+1 and nilpotency class p, but is not a regular p-group. Since groups of order pp are always regular groups, it is also a minimal such example.
Generalized dihedral groups
When p=2 and n=2, W(n) is the dihedral group of order 8, so in some sense W(n) provides an analogue for the dihedral group for all primes p when n=2. However, for higher n the analogy becomes strained. There is a different family of examples that more closely mimics the dihedral groups of order 2n, but that requires a bit more setup. Let ζ denote a primitive pth root of unity in the complex numbers, and let Z[ζ] be the ring of cyclotomic integers generated by it, and let P be the prime ideal generated by 1−ζ. Let G be a cyclic group of order p generated by an element z. Form the semidirect product E(p) of Z[ζ] and G where z acts as multiplication by ζ. The powers Pn are normal subgroups of E(p), and the example groups are E(p,n) = E(p)/Pn. E(p,n) has order pn+1 and nilpotency class n, so is a p-group of maximal class. When p=2, E(2,n) is the dihedral group of order 2n. When p is odd, both W(2) and E(p,p) are irregular groups of maximal class and order pp+1, but are not isomorphic.
Unitriangular matrix groups
The Sylow subgroups of general linear groups are another fundamental family of examples. Let V be a vector space of dimension n with basis { e1, e2, …, en } and define Vi to be the vector space generated by { ei, ei+1, …, en } for 1 ≤ i ≤ n, and define Vi = 0 when i > n. For each 1 ≤ m ≤ n, the set of invertible linear transformations of V which take each Vi to Vi+m form a subgroup of Aut(V) denoted Um. If V is a vector space over Z/pZ, then U1 is a Sylow p-subgroup of Aut(V) = GL(n, p), and the terms of its lower central series are just the Um. In terms of matrices, Um are those upper triangular matrices with 1s one the diagonal and 0s on the first m−1 superdiagonals. The group U1 has order pn·(n−1)/2, nilpotency class n, and exponent pk where k is the least integer at least as large as the base p logarithm of n.
Classification
The groups of order pn for 0 ≤ n ≤ 4 were classified early in the history of group theory (Burnside 1897), and modern work has extended these classifications to groups whose order divides p7, though the sheer number of families of such groups grows so quickly that further classifications along these lines are judged difficult for the human mind to comprehend (Leedham-Green & McKay 2002, p. 214). An example is (Hall & Senior 1964), which classifies groups of order 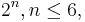 .
.
Rather than classify the groups by order, Philip Hall proposed using a notion of isoclinism of groups which gathered finite p-groups into families based on large quotient and subgroups (Hall 1940).
An entirely different method classifies finite p-groups by their coclass, that is, the difference between their composition length and their nilpotency class. The so-called coclass conjectures described the set of all finite p-groups of fixed coclass as perturbations of finitely many pro-p groups. The coclass conjectures were proven in the 1980s using techniques related to Lie algebras and powerful p-groups (Leedham-Green & McKay 2002).
Prevalence
Among groups
The number of isomorphism classes of groups of order pn grows as 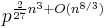 , and these are dominated by the classes that are two-step nilpotent (Sims 1965). Because of this rapid growth, there is a folklore conjecture asserting that almost all finite groups are 2-groups: the fraction of isomorphism classes of 2-groups among isomorphism classes of groups of order at most n is thought to tend to 1 as n tends to infinity. For instance, of the 49 910 529 484 different groups of order at most 2000, 49 487 365 422, or just over 99%, are 2-groups of order 1024 (Besche, Eick & O'Brien 2002).
, and these are dominated by the classes that are two-step nilpotent (Sims 1965). Because of this rapid growth, there is a folklore conjecture asserting that almost all finite groups are 2-groups: the fraction of isomorphism classes of 2-groups among isomorphism classes of groups of order at most n is thought to tend to 1 as n tends to infinity. For instance, of the 49 910 529 484 different groups of order at most 2000, 49 487 365 422, or just over 99%, are 2-groups of order 1024 (Besche, Eick & O'Brien 2002).
Within a group
Every finite group whose order is divisible by p contains a subgroup which is a non-trivial p-group, namely a cyclic group of order p generated by an element of order p obtained from Cauchy's theorem. In fact, it contains a p-group of maximal possible order: if 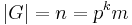 where p does not divide m, then G has a subgroup P of order
where p does not divide m, then G has a subgroup P of order 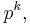 called a Sylow p-subgroup. This subgroup need not be unique, but any subgroups of this order are conjugate, and any p-subgroup of G is contained in a Sylow p-subgroup. This and other properties are proved in the Sylow theorems.
called a Sylow p-subgroup. This subgroup need not be unique, but any subgroups of this order are conjugate, and any p-subgroup of G is contained in a Sylow p-subgroup. This and other properties are proved in the Sylow theorems.
Application to structure of a group
p-groups are fundamental tools in understanding the structure of groups and in the classification of finite simple groups. p-groups arise both as subgroups and as quotient groups. As subgroups, for a given prime p one has the Sylow p-subgroups P (largest p-subgroup not unique but all conjugate) and the p-core  (the unique largest normal p-subgroup), and various others. As quotients, the largest p-group quotient is the quotient of G by the p-residual subgroup
(the unique largest normal p-subgroup), and various others. As quotients, the largest p-group quotient is the quotient of G by the p-residual subgroup 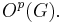 These groups are related (for different primes), possess important properties such as the focal subgroup theorem, and allow one to determine many aspects of the structure of the group.
These groups are related (for different primes), possess important properties such as the focal subgroup theorem, and allow one to determine many aspects of the structure of the group.
Local control
Much of the structure of a finite group is carried in the structure of its so-called local subgroups, the normalizers of non-identity p-subgroups (Glauberman 1971).
The large elementary abelian subgroups of a finite group exert control over the group that was used in the proof of the Feit–Thompson theorem. Certain central extensions of elementary abelian groups called extraspecial groups help describe the structure of groups as acting symplectic vector spaces.
Brauer classified all groups whose Sylow 2-subgroups are the direct product of two cyclic groups of order 4, and Walter, Gorenstein, Bender, Suzuki, Glauberman, and others classified those simple groups whose Sylow 2-subgroups were abelian, dihedral, semidihedral, or quaternion.
See also
Notes
- ^ To prove that a group of order p2 is abelian, note that it is a p-group so has non-trivial center, so given a non-trivial element of the center g, this either generates the group (so G is cyclic, hence abelian:
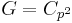 ), or it generates a subgroup of order p, so g and some element h not in its orbit generate G, (since the subgroup they generate must have order
), or it generates a subgroup of order p, so g and some element h not in its orbit generate G, (since the subgroup they generate must have order 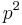 ) but they commute since g is central, so the group is abelian, and in fact
) but they commute since g is central, so the group is abelian, and in fact 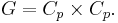
References
- Besche, Hans Ulrich; Eick, Bettina; O'Brien, E. A. (2002), "A millennium project: constructing small groups", International Journal of Algebra and Computation 12 (5): 623–644, doi:10.1142/S0218196702001115, MR1935567
- Burnside, William (1897), Theory of groups of finite order, Cambridge University Press, http://books.google.com/?id=yBgPAAAAIAAJ&printsec=titlepage
- Glauberman, George (1971), "Global and local properties of finite groups", Finite simple groups (Proc. Instructional Conf., Oxford, 1969), Boston, MA: Academic Press, pp. 1–64, MR0352241
- Hall, Jr., Marshall; Senior, James K. (1964), The Groups of Order 2n (n ≤ 6), Macmillan, LCCN 6416861, MR168631. An exhaustive catalog of the 340 groups of order dividing 64 with detailed tables of defining relations, constants, and lattice presentations of each group in the notation the text defines. "Of enduring value to those interested in finite groups" (from the preface).
- Hall, Philip (1940), "The classification of prime-power groups", Journal für die reine und angewandte Mathematik 182 (182): 130–141, doi:10.1515/crll.1940.182.130, ISSN 0075-4102, MR0003389, http://resolver.sub.uni-goettingen.de/purl?GDZPPN00217491X
- Leedham-Green, C. R.; McKay, Susan (2002), The structure of groups of prime power order, London Mathematical Society Monographs. New Series, 27, Oxford University Press, ISBN 978-0-19-853548-5, MR1918951
- Sims, Charles (1965), "Enumerating p-groups", Proc. London Math. Soc. (3) 15: 151–166, doi:10.1112/plms/s3-15.1.151, MR0169921
- Y. Berkovich, Groups of Prime Power Order, Volume 1, W. de Gruyter, Berlin, 2008.
- Y. Berkovich and Z. Janko, Groups of Prime Power Order, Volume 2, W. de Gruyter, Berlin, 2008.