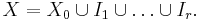o-minimal theory
In mathematical logic, and more specifically in model theory, an infinite structure (M,<,...) which is totally ordered by < is called an o-minimal structure if and only if every definable subset X ⊂ M (with parameters taken from M) is a finite union of intervals and points.
O-minimality can be regarded as a weak form of quantifier elimination. A structure M is o-minimal if and only if every formula with one free variable and parameters in M is equivalent to a quantifier-free formula involving only the ordering, also with parameters in M. This is analogous to the minimal structures, which are exactly the analogous property down to equality.
A theory T is an o-minimal theory if every model of T is o-minimal. Pillay can show that the complete theory T of an o-minimal structure is an o-minimal theory. This result is remarkable because the complete theory of a minimal structure need not be a strongly minimal theory, that is, there may be an elementarily equivalent structure which is not minimal.
Contents |
Set-theoretic definition
O-minimal structures can be defined without recourse to model theory. Here we define a structure on a nonempty set M in a set-theoretic manner, as a sequence S = (Sn), n = 0,1,2,... such that
- Sn is a boolean algebra of subsets of Mn
- if A ∈ Sn then M × A and A ×M are in Sn+1
- the set {(x1,...,xn) ∈ Mn : x1 = xn} is in Sn
- if A ∈ Sn+1 and π : Mn+1 → Mn is the projection map on the first n coordinates, then π(A) ∈ Mn.
If M has a dense linear order without endpoints on it, say <, then a structure S on M is called o-minimal if it satisfies the extra axioms
- the set {(x,y) ∈ M2 : x < y} is in S2
- the sets in S1 are precisely the finite unions of intervals and points.
The "o" stands for "order", since any o-minimal structure requires an ordering on the underlying set.
Model theoretic definition
O-minimal structures originated in model theory and so have a simpler — but equivalent — definition using the language of model theory. Specifically if L is a language including a binary relation <, and (M,<,...) is an L-structure where < is interpreted to satisfy the axioms of a dense linear order,[1] then (M,<,...) is called an o-minimal structure if for any definable set X ⊆ M there are finitely many intervals I1,...,Ir with endpoints in M ∪ {±∞} and a finite set X0 such that
Examples
Examples of o-minimal theories are:
- RCF, the theory of real closed fields;
- The complete theory of the real field with a symbol for the exponential function by Wilkie's theorem;
- The complete theory of the real numbers with restricted analytic functions added (i.e. analytic functions on a neighborhood of [0,1]n, restricted to [0,1]n; note that the unrestricted sine function has infinitely many roots, and so cannot be definable in a o-minimal structure.)
- Intermediate to the previous two examples is the complete theory of the real numbers with restricted Pfaffian functions added.
- The complete theory of dense linear orders in the language with just the ordering.
In the first example, the definable sets are the semialgebraic sets. Thus the study of o-minimal structures and theories generalises Real algebraic geometry. A major line of current research is based on discovering expansions of the real ordered field that are o-minimal. Despite the generality of application, one can show a great deal about the geometry of set definable in o-minimal structures. There is a cell decomposition theorem, Whitney and Verdier stratification theorems and a good notion of dimension and Euler characteristic.
See also
- Semialgebraic set
- Real algebraic geometry
- Strongly minimal theory
- Weakly o-minimal structure
- C-minimal theory
Notes
References
- van den Dries, Lou (1998). Tame Topology and o-minimal Structures. Cambridge University Press.
- Marker, David (2000). "Review of "Tame Topology and o-minimal Structures"". Bulletin of the American Mathematical Society 37 (3): 351–357. doi:10.1090/S0273-0979-00-00866-1. http://www.ams.org/bull/2000-37-03/S0273-0979-00-00866-1/S0273-0979-00-00866-1.pdf.
- Pillay, Anand; Steinhorn, Charles (1986). "Definable Sets in Ordered Structures I". Transactions of the American Mathematical Society (Transactions of the American Mathematical Society, Vol. 295, No. 2) 295 (2): 565–592. doi:10.2307/2000052. JSTOR 2000052. http://www.ams.org/bull/1984-11-01/S0273-0979-1984-15251-0/S0273-0979-1984-15251-0.pdf.
- Knight, Julia; Pillay, Anand; Steinhorn, Charles (1986). "Definable Sets in Ordered Structures II". Transactions of the American Mathematical Society (Transactions of the American Mathematical Society, Vol. 295, No. 2) 295 (2): 593–605. doi:10.2307/2000053. JSTOR 2000053.
- Pillay, Anand; Steinhorn, Charles (1988). "Definable Sets in Ordered Structures III". Transactions of the American Mathematical Society (Transactions of the American Mathematical Society, Vol. 309, No. 2) 309 (2): 469–476. doi:10.2307/2000920. JSTOR 2000920.
- Wilkie, A.J. (1996). "Model completeness results for expansions of the ordered field of real numbers by restricted Pfaffian functions and the exponential function". Journal of the American Mathematical Society 9 (4): 1051. doi:10.1090/S0894-0347-96-00216-0. https://www.ams.org/jams/1996-9-04/S0894-0347-96-00216-0/S0894-0347-96-00216-0.pdf.
- Denef, J.; van den Dries, L. (1989). "p-adic and real subanalytic sets". Annals of Mathematics 54 (1): 79–138. JSTOR 1971463.