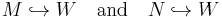h-cobordism

A cobordism W between M and N is an h-cobordism (the h stands for homotopy equivalence) if the inclusion maps

M \hookrightarrow W \quad\mbox{and}\quad N \hookrightarrow W

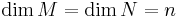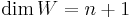are homotopy equivalences. If \mbox{dim}\,M = \mbox{dim}\,N = n and \mbox{dim}\,W = n%2B1, it is called an 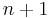n%2B1-dimensional h-cobordism.[1]

The h-cobordism theorem states that if:

then W is Cat-isomorphic[2] to M × [0, 1] and (hence) M is Cat-isomorphic to N. Informally, "a simply connected h-cobordism is a cylinder".

The theorem was first proved by Stephen Smale and is the fundamental result in the theory of high-dimensional manifolds: for a start, it almost immediately proves the Generalized Poincaré Conjecture. The theorem is still true topologically but not smoothly for n = 4; a later result of Michael Freedman.

Before Smale proved this theorem, mathematicians had got stuck trying to understand manifolds of dimension 3 or 4, and assumed that the higher-dimensional cases were even harder. The h-cobordism theorem showed that (simply connected) manifolds of dimension at least 5 are much easier than those of dimension 3 or 4. The proof of the theorem depends on the "Whitney trick" of Hassler Whitney, which geometrically untangles homologically-tangled spheres of complementary dimension in a manifold of dimension >5. An informal reason why manifolds of dimension 3 or 4 are unusually hard is that the trick fails to work in lower dimensions, which have no room for untanglement, and so have more tangles.

Contents

Low dimensions

For n = 4, the h-cobordism theorem is true topologically (proved by Michael Freedman using a 4-dimensional Whitney trick) but is false PL and smoothly (as shown by Simon Donaldson).

For n = 3, the h-cobordism theorem for smooth manifolds has not been proved and, due to the Poincaré conjecture, is equivalent to the hard open question of whether the 4-sphere has non-standard smooth structures.

For n = 2, the h-cobordism theorem[3] is true – it is equivalent to the Poincaré conjecture, which has been proved by Grigori Perelman.

For n = 1, h-cobordism theorem is vacuously true, since there is no closed simply-connected 1-dimensional manifold.

For n = 0, the h-cobordism theorem is trivially true: the interval is the only connected cobordism between connected 0-manifolds.

The s-cobordism theorem

If the assumption that M and N are simply connected is dropped, h-cobordisms need not be cylinders; the obstruction is exactly the Whitehead torsion τ (W, M) of the inclusion 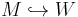M \hookrightarrow W.

Precisely, the s-cobordism theorem (the s stands for simple-homotopy equivalence), proved independently by Barry Mazur, John Stallings, and Dennis Barden, states (assumptions as above but where M and N need not be simply connected):

an h-cobordism is a cylinder if and only if Whitehead torsion τ (W, M) vanishes

The torsion vanishes if and only if the inclusion 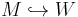M \hookrightarrow W is not just a homotopy equivalence, but a simple homotopy equivalence.

Note that one need not assume that the other inclusion 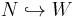N \hookrightarrow W is also a simple homotopy equivalence—that follows from the theorem.

Categorically, h-cobordisms form a groupoid.

Then a finer statement of the s-cobordism theorem is that the isomorphism classes of this category (up to Cat-isomorphism of h-cobordisms) are torsors for the respective[4] Whitehead groups 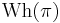\mbox{Wh}(\pi), where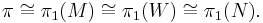 \pi \cong \pi_1(M) \cong \pi_1(W) \cong \pi_1(N).

Notes

  1. ^ This notation is to clarify the dimension of all manifolds in question, otherwise it is unclear whether a "5-dimensional h-cobordism" refers to a 5-dimensional cobordism between 4-dimensional manifolds or a 6-dimensional cobordism between 5-dimensional manifolds.
  2. ^ So diffeomorphic, PL-isomorphic, homeomorphic.
  3. ^ In 3 dimensions and below, the categories are the same: Diff=PL=Top.
  4. ^ Note that identifying the Whitehead groups of the various manifolds requires that one choose base points 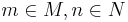m\in M, n\in N and a path in W connecting them.

See also

References