Zocchihedron
Zocchihedron is the trademark of a 100-sided die invented by Lou Zocchi, which debuted in 1985. Rather than being a polyhedron, it is more like a ball with 100 flattened planes. It is sometimes called "Zocchi's Golfball".
Zocchihedra are designed to handle percentage rolls in games, particularly in role-playing games.
Contents |
History
It took three years for Zocchi to design his dice, and three more years to get it into production. Zocchi discovered that the dice would perform best at a depth of 13.85 mm. Since its introduction Zocchi has improved the design of the Zocchihedron, filling it with teardrop-shaped free-falling weights to make it settle more swiftly when rolled.
The Zocchihedron II is a further improved model, and has another filler.
Probability distribution of rolls
A test published in White Dwarf magazine concluded that the frequency distribution of the Zocchihedron was substantially uneven.[1] Jason Mills performed 5,164 rolls[2] and found that results more than 93 or less than 8 are significantly rarer than middling results. Mills attributed this to the placement of the extreme numbers near the poles of the zocchihedron, where they are closer together. Numbers near the equator are more widely spaced.
Later versions of the Zocchihedron have been designed with a different pattern of number distribution, resulting in more even results overall.
Patents
The aesthetic appearance of the Zocchihedron was protected by United States design patent D303,553,[3] which expired on 19 September 2003. There was never a utility patent for the original Zocchihedron, although United States patent 6,926,276[4] may protect the braking mechanism of the Zocchihedron II. That patent will expire on 9 August 2025 and applies only to 100-sided dice containing "multi sized and irregularly shaped particles."
Notes
- ^ White Dwarf 85, January 1987 Text of letter and photo of graph at FreakyTrigger.co.uk
- ^ Binomial distribution dictates that, to be confident of an average result on a right die, the number of trials required is the mean divided by the probability of a given result. Here the mean is
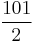 and the relevant probability is 1/100, so the number of trials required is 5050.
and the relevant probability is 1/100, so the number of trials required is 5050. - ^ United States Patent: D303553 (Patent Full Text and Image Database)
- ^ United States Patent: 6926276 (Patent Full Text and Image Database)