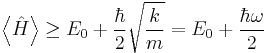Zero-point energy
Zero-point energy is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state. All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature. The uncertainty principle requires every physical system to have a zero-point energy greater than the minimum of its classical potential well, even at absolute zero. For example, liquid helium does not freeze under atmospheric pressure at any temperature because of its zero-point energy.
The concept of zero-point energy was developed in Germany by Albert Einstein and Otto Stern in 1913, using a formula developed by Max Planck in 1900.[1][2] The term zero-point energy originates from the German Nullpunktsenergie.[1][2] The German name is also spelled Nullpunktenergie (without the "s").
Vacuum energy is the zero-point energy of all the fields in space, which in the Standard Model includes the electromagnetic field, other gauge fields, fermionic fields, and the Higgs field. It is the energy of the vacuum, which in quantum field theory is defined not as empty space but as the ground state of the fields. In cosmology, the vacuum energy is one possible explanation for the cosmological constant.[3] A related term is zero-point field, which is the lowest energy state of a particular field.[4]
Contents |
History
In 1900, Max Planck derived the formula for the energy of a single energy radiator, e.g. a vibrating atomic unit:[5]
where  is Planck's constant,
is Planck's constant,  is the frequency, k is Boltzmann's constant, and T is the absolute temperature.
is the frequency, k is Boltzmann's constant, and T is the absolute temperature.
Then in 1913, using this formula as a basis, Albert Einstein and Otto Stern published a paper of great significance in which they suggested for the first time the existence of a residual energy that all oscillators have at absolute zero. They called this residual energy Nullpunktsenergie (German), later translated as zero-point energy. They carried out an analysis of the specific heat of hydrogen gas at low temperature, and concluded that the data are best represented if the vibrational energy is[1][2]
According to this expression, an atomic system at absolute zero retains an energy of ½hν.
In 1916 Walther Nernst postulated that the vacuum of space is filled with zero-point electromagnetic radiation.
Relation to the uncertainty principle
Zero-point energy is fundamentally related to the Heisenberg uncertainty principle. Roughly speaking, the uncertainty principle states that complementary variables (such as a particle's position and momentum, or a field's value and derivative at a point in space) cannot simultaneously be defined precisely by any given quantum state. In particular, there cannot be a state in which the system sits motionless at the bottom of its potential well, for then its position and momentum would both be completely determined to arbitrarily great precision. Therefore, the lowest-energy state (the ground state) of the system must have a distribution in position and momentum that satisfies the uncertainty principle, which implies its energy must be greater than the minimum of the potential well.
Near the bottom of a potential well, the Hamiltonian of a system (the quantum-mechanical operator giving its energy) can be approximated as
where 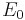 is the minimum of the classical potential well. The uncertainty principle tells us that
is the minimum of the classical potential well. The uncertainty principle tells us that
making the expectation values of the kinetic and potential terms above satisfy
The expectation value of the energy must therefore be at least
where  is the angular frequency at which the system oscillates.
is the angular frequency at which the system oscillates.
A more thorough treatment, showing that the energy of the ground state actually is  requires solving for the ground state of the system. See quantum harmonic oscillator for details.
requires solving for the ground state of the system. See quantum harmonic oscillator for details.
Varieties
The concept of zero-point energy occurs in a number of situations.
In ordinary quantum mechanics, the zero-point energy is the energy associated with the ground state of the system. The professional physics literature tends to measure frequency, as denoted by  above, using angular frequency, denoted with
above, using angular frequency, denoted with  and defined by
and defined by  =
= 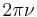 . This leads to a convention of writing Planck's constant
. This leads to a convention of writing Planck's constant  with a bar through its top to denote the quantity
with a bar through its top to denote the quantity  /
/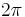 . In those terms, the most famous such example of zero-point energy is
. In those terms, the most famous such example of zero-point energy is  associated with the ground state of the quantum harmonic oscillator. In quantum mechanical terms, the zero-point energy is the expectation value of the Hamiltonian of the system in the ground state.
associated with the ground state of the quantum harmonic oscillator. In quantum mechanical terms, the zero-point energy is the expectation value of the Hamiltonian of the system in the ground state.
In quantum field theory, the fabric of space is visualized as consisting of fields, with the field at every point in space and time being a quantum harmonic oscillator, with neighboring oscillators interacting. In this case, one has a contribution of  from every point in space, resulting in a calculation of infinite zero-point energy in any finite volume; this is one reason renormalization is needed to make sense of quantum field theories. The zero-point energy is again the expectation value of the Hamiltonian; here, however, the phrase vacuum expectation value is more commonly used, and the energy is called the vacuum energy.
from every point in space, resulting in a calculation of infinite zero-point energy in any finite volume; this is one reason renormalization is needed to make sense of quantum field theories. The zero-point energy is again the expectation value of the Hamiltonian; here, however, the phrase vacuum expectation value is more commonly used, and the energy is called the vacuum energy.
In quantum perturbation theory, it is sometimes said that the contribution of one-loop and multi-loop Feynman diagrams to elementary particle propagators are the contribution of vacuum fluctuations or the zero-point energy to the particle masses.
Experimental observations
A phenomenon that is commonly presented as evidence for the existence of zero-point energy in vacuum is the Casimir effect, proposed in 1948 by Dutch physicist Hendrik B. G. Casimir (Philips Research), who considered the quantized electromagnetic field between a pair of grounded, neutral metal plates. The vacuum energy contains contributions from all wavelengths, except those excluded by the spacing between plates. As the plates draw together, more wavelengths are excluded and the vacuum energy decreases. The decrease in energy means there must be a force doing work on the plates as they move. This force has been measured and found to be in good agreement with the theory. However, there is still some debate on whether vacuum energy is necessary to explain the Casimir effect. Robert Jaffe of MIT argues that the Casimir force should not be considered evidence for vacuum energy, since it can be derived in QED without reference to vacuum energy by considering charge-current interactions (the radiation-reaction picture).[6]
The experimentally measured Lamb shift has been argued to be, in part, a zero-point energy effect.[7]
Gravitation and cosmology
| Why doesn't the zero-point energy density of the vacuum change with changes in the volume of the universe? And related to that, why doesn't the large constant zero-point energy density of the vacuum cause a large cosmological constant? What cancels it out? |
In cosmology, the zero-point energy offers an intriguing possibility for explaining the speculative positive values of the proposed cosmological constant. In brief, if the energy is "really there", then it should exert a gravitational force.[8] In general relativity, mass and energy are equivalent; both produce a gravitational field. One obvious difficulty with this association is that the zero-point energy of the vacuum is absurdly large. Naively, it is infinite, because it includes the energy of waves with arbitrarily short wavelengths. But since only differences in energy are physically measurable, the infinity can be removed by renormalization. In all practical calculations, this is how the infinity is handled. It is also arguable that undiscovered physics relevant at the Planck scale reduces or eliminates the energy of waves shorter than the Planck length, making the total zero-point energy finite.
Free-energy devices
As a scientific concept, the existence of zero-point energy is not controversial although the ability to harness it is. In particular, perpetual motion machines and other power generating devices supposedly based on zero-point energy are highly controversial and, in many cases, in violation of some of the fundamental laws of physics. No device claimed to operate using zero-point energy has been demonstrated to operate as claimed.. However, many engineers claim to have invented such over-unity devices, and at least one plausible description of a device drawing useful power from a source of zero-point energy has been given. [9]
Thus, current claims to zero-point-energy-based power generation systems have the status of pseudoscience.[10]
The discovery of zero-point energy did not alter the implausibility of perpetual motion machines. Much attention has been given to reputable science suggesting that zero-point-energy density is infinite, but in quantum theory, zero-point energy is a minimum energy below which a thermodynamic system can never go. Thus according to the standard quantum-theoretic viewpoint, none of this energy can be withdrawn without altering the system to a different form in which the system has a lower zero-point energy.
It is possible that the discovery of new physics will alter this conclusion. For example, in stochastic electrodynamics, the zero-point field is viewed as simply a classical background isotropic noise wave field which excites all systems present in the vacuum and thus is responsible for their minimum-energy or "ground" states. The requirement of Lorentz invariance at a statistical level then implies that the energy density spectrum must increase with the third power of frequency, implying infinite energy density when integrated over all frequencies.[11] If this theory is correct, there is no reason that energy, or for that matter, momentum, could not be extracted, and would of course still leave infinite energy density and infinite momentum density, isotropic in all directions simultaneously, remaining in the wave field.
According to NASA, "the concept of accessing a significant amount of useful energy from the ZPE gained much credibility when a major article on this topic was recently [March 1st, 2004] published in Aviation Week & Space Technology, a leading aerospace industry magazine".[12]
The calculation that underlies the Casimir experiment, a calculation based on the formula predicting infinite vacuum energy, shows the zero-point energy of a system consisting of a vacuum between two plates will decrease at a finite rate as the two plates are drawn together. The vacuum energies are predicted to be infinite, but the changes are predicted to be finite. Casimir combined the projected rate of change in zero-point energy with the principle of conservation of energy to predict a force on the plates. The predicted force, which is very small and was experimentally measured to be within 5% of its predicted value, is finite.[13] Even though the zero-point energy is theoretically infinite, there is as yet no practical evidence to suggest that infinite amounts of zero-point energy are available for use, that zero-point energy can be withdrawn for free, or that zero-point energy can be used in violation of conservation of energy.[14]
Notes
- ^ a b c Laidler, K. J. (2001). The World of Physical Chemistry. Oxford University Press. p. 324. ISBN 0198559194.
- ^ a b c {Einstein, A.; Stern, O. (1913). "Einige Argumente für die Annahme einer molekularen Agitation beim absoluten Nullpunkt". Annalen der Physik 40 (3): 551. Bibcode 1913AnP...345..551E. doi:10.1002/andp.19133450309.
- ^ Rugh, S. E.; Zinkernagel, H. (2002). "The Quantum Vacuum and the Cosmological Constant Problem". Studies in History and Philosophy of Modern Physics, vol. 33 (4): 663–705. arXiv:hep-th/0012253. doi:10.1016/S1355-2198(02)00033-3.
- ^ Gribbin, J. (1998). Q is for Quantum: An Encyclopedia of Particle Physics. Touchstone Books. ISBN 0-684-86315-4.
- ^ Planck, M (1900). "Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum". Verhandlungen der Deutschen Physikalischen Gesellschaft 2: 237–245.
- ^ Jaffe, R. L. (2005). Physical Review D 72 (2): 021301.
- ^ Hawton, M. (1993). "Self-consistent frequencies of the electron-photon system". Physical Review A 48 (3): 1824. Bibcode 1993PhRvA..48.1824H. doi:10.1103/PhysRevA.48.1824.
- ^ Zee, A. (2008). "Gravity and Its Mysteries: Some Thoughts and Speculations". AAPPS Bulletin 18 (4): 32. http://www.cospa.ntu.edu.tw/aappsbulletin/data/18-4/06_Gravity.pdf.
- ^ [http://jnaudin.free.fr/meg/megpaper.pdf "The Motionless Electromagnetic Generator: Extracting Energy from a Permanent Magnet with Energy-Replenishing from the Active Vacuum"]. T.E. Bearden et al.. http://jnaudin.free.fr/meg/megpaper.pdf.
- ^ "Zero-Point Energy: Can We Get Something From Nothing". U.S. Army National Ground Intelligence Center. http://www.scribd.com/doc/297161/Zero-Point-Energy.
- ^ de la Peña, L.; Cetto, A. M. (1995). The Quantum Dice: An Introduction to Stochastic Electrodynamics. ISBN 978-0792338185.
- ^ Advanced Energetics for Aeronautical Applications: Volume II. NASA. http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20050170447_2005172301.pdf.
- ^ "What is the Casimir Effect?". http://math.ucr.edu/home/baez/physics/Quantum/casimir.html.
- ^ "FOLLOW-UP: What is the 'zero-point energy' (or 'vacuum energy') in quantum physics? Is it really possible that we could harness this energy?". Scientific American. 18 August 1997. http://www.sciam.com/article.cfm?id=follow-up-what-is-the-zer.
Bibliography
- Beiser, A. (1967). Concepts of Modern Physics. McGraw-Hill. ISBN 0070044732.
- Einstein, A.; Hopf, L. (1910). "On a theorem of the probability calculus and its application to the theory of radiation". Annalen der Physik 33 (16): 1096–1104. Bibcode 1910AnP...338.1096E. doi:10.1002/andp.19103381603.
- Einstein, A.; Hopf, L. (1910). "Statistical investigation of a resonator' s motion in a radiation field". Annalen der Physik 33 (16): 1105–1115. Bibcode 1910AnP...338.1105E. doi:10.1002/andp.19103381604.
- Einstein, A.; Stern, O. (1913). "Einige Argumente für die Annahme einer molekularen Agitation beim absoluten Nullpunkt". Annalen der Physik 40 (3): 551. Bibcode 1913AnP...345..551E. doi:10.1002/andp.19133450309.
- Haisch, B.; Rueda, A.; Dobyns, Y. (2001). "Inertial mass and the quantum vacuum fields". Annalen der Physik 10 (5): 393–414. arXiv:gr-qc/0009036. Bibcode 2001AnP...513..393H. doi:10.1002/1521-3889(200105)10:5<393::AID-ANDP393>3.0.CO;2-Z. http://www.calphysics.org/articles/annalen.pdf.
- Loudon, R. (2000). The Quantum Theory of Light (3rd ed.). Clarendon Press. ISBN 0-19-850176-5.
- Milonni, P. W. (1994). The Quantum Vacuum: An Introduction to Quantum Electrodynamics. Academic Press. ISBN 0-12-498080-5.
- Nernst, W. (1916). "Über einen Versuch, von quantentheoretischen Betrachtungen zur Annahme stetiger Energieänderungen zurückzukehren". Verhandlungen der Deutschen Physikalischen Gesellschaft 18: 83.
- Sciama, D. W. (1991). Saunders, S.; Brown, H. R.. eds. The Philosophy of Vacuum. Clarendon Press. ISBN 0-19-824449-5.
- Rafelski, J.; Muller, B. (1985). The Structured Vacuum: Thinking about nothing. Harri Deutsch. ISBN 3-87144-889-3. http://www.physics.arizona.edu/~rafelski/Books/StructVacuumE.pdf.
- Boyer, T. H. (1968). "Quantum Electromagnetic Zero-Point Energy of a Conducting Spherical Shell and the Casimir Model for a Charged Particle". Physical Review 174 (5): 13. Bibcode 1968PhRv..174.1764B. doi:10.1103/PhysRev.174.1764. http://www.mit.edu/~kardar/research/seminars/Casimir/PR-Boyer68.pdf.
- Yablonovitch, E. (1989). "Accelerating Reference Frame for Electromagnetic Waves in a Rapidly Growing Plasma: Unruh-Davies-Fulling-DeWitt Radiation and the Nonadiabatic Casimir Effect". Physical Review Letters 62 (15): 1742–1745. Bibcode 1989PhRvL..62.1742Y. doi:10.1103/PhysRevLett.62.1742. PMID 10039756. http://www.ee.ucla.edu/~photon/pubs/ey1989prl6215.pdf.
External links
- Zero-point energy? "Ask the Van" popular science FAQ at University of Illinois.
- Philip Yam, "Exploiting Zero-point Energy", Scientific American Magazine, December 1997, pp. 82–85.
- Matt Visser, What is the 'zero-point energy' (or 'vacuum energy') in quantum physics? Is it really possible that we could harness this energy? from Scientific American Magazine, August 18, 1997
- Calphysics Institute "Zero Point Energy and Zero Point Field"