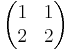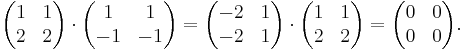Zero divisor

In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0.^[1] Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply called a zero divisor. If multiplication in the ring is commutative, then the left and right zero divisors are the same. A nonzero element of a ring that is neither a left nor right zero divisor is called regular.

1 Examples
2 Properties
3 See also
4 Notes
5 References

Examples

The ring Z of integers has no zero divisors, but in the ring Z × Z with componentwise addition and multiplication, (0,1)·(1,0) = (0,0), so both (0,1) and (1,0) are zero divisors.
An example of a zero divisor in the ring of 2-by-2 matrices is the matrix

$\begin{pmatrix}1&1\\ 2&2\end{pmatrix}$

because for instance

$\begin{pmatrix}1&1\\ 2&2\end{pmatrix}\cdot\begin{pmatrix}1&1\\ -1&-1\end{pmatrix}=\begin{pmatrix}-2&1\\ -2&1\end{pmatrix}\cdot\begin{pmatrix}1&1\\ 2&2\end{pmatrix}=\begin{pmatrix}0&0\\ 0&0\end{pmatrix}.$

More generally in the ring of n-by-n matrices over some field, the left and right zero divisors coincide; they are precisely the nonzero singular matrices. In the ring of n-by-n matrices over some integral domain, the zero divisors are precisely the nonzero matrices with determinant zero.

Here is an example of a ring with an element that is a zero divisor on one side only. Let S be the set of all sequences of integers (a₁, a₂, a₃...). Take for the ring all additive maps from S to S, with pointwise addition and composition as the ring operations. (That is, our ring is End(S), the endomorphisms of the additive group S.) Three examples of elements of this ring are the right shift R(a₁, a₂, a₃,...) = (0, a₁, a₂,...), the left shift L(a₁, a₂, a₃,... ) = (a₂, a₃,...), and a third additive map T(a₁, a₂, a₃,... ) = (a₁, 0, 0, ... ). All three of these additive maps are not zero, and the composites LT and TR are both zero, so L is a left zero divisor and R is a right zero divisor in the ring of additive maps from S to S. However, L is not a right zero divisor and R is not a left zero divisor: the composite LR is the identity, so if some additive map f from S to S satisfies fL= 0 then composing both sides of this equation on the right with R shows (fL)R = f(LR) = f1 = f has to be 0, and similarly if some f satisfies Rf = 0 then composing both sides on the left with L shows f is 0.

Continuing with this example, note that while RL is a left zero divisor ((RL)T = R(LT) is 0 because LT is), LR is not a zero divisor on either side because it is the identity.

Concretely, we can interpret additive maps from S to S as countably infinite matrices. The matrix

$A = \begin{pmatrix} 0 & 1 & 0 &0&0&\\ 0 & 0 & 1 &0&0&\cdots\\ 0 & 0 & 0 &1&0&\\ 0&0&0&0&1&\\ &&\vdots&&&\ddots \end{pmatrix}$

realizes L explicitly (just apply the matrix to a vector and see the effect is exactly a left shift) and the transpose B = A^T realizes the right shift on S. That AB is the identity matrix is the same as saying LR is the identity. In particular, as matrices A is a left zero divisor but not a right zero divisor.

Properties

Left or right zero divisors can never be units, because if a is invertible and ab = 0, then 0 = a⁻¹0 = a⁻¹ab = b.

Every nonzero idempotent element a ≠ 1 is a zero divisor, since a² = a implies a(a − 1) = (a − 1)a = 0. Nonzero nilpotent ring elements are also trivially zero divisors.

A commutative ring with 0 ≠ 1 and without zero divisors is called an integral domain.

Zero divisors occur in the quotient ring Z/nZ if and only if n is composite. When n is prime, there are no zero divisors and this ring is, in fact, a field, as every nonzero element is a unit.

Zero divisors also occur in the sedenions, or 16-dimensional hypercomplex numbers under the Cayley–Dickson construction.

The set of zero divisors is the union of the associated prime ideals of the ring.

Notes

^ See Hazewinkel et. al. (2004), p. 2.

References

Michiel Hazewinkel, Nadiya Gubareni, Nadezhda Mikhaĭlovna Gubareni, Vladimir V. Kirichenko. Algebras, rings and modules. Volume 1. 2004. Springer, 2004. ISBN 1-4020-2690-0
Weisstein, Eric W., "Zero Divisor" from MathWorld.

Zero divisor

Contents

Examples

Properties

See also

Notes

References