Xorshift

Xorshift random number generators form a class of pseudorandom number generators that was discovered by George Marsaglia.[1] They generate the next number in their sequence by repeatedly taking the exclusive or of a number with a bit shifted version of itself. This makes them extremely fast on modern computer architectures. They are a subclass of Linear feedback shift registers, but their simple implementation typically makes them faster and use less space.[2]

Contents

Example Implementation

A C version[note 1] of one xorshift algorithm [1] is:

uint32_t xor128(void) {
  static uint32_t x = 123456789;
  static uint32_t y = 362436069;
  static uint32_t z = 521288629;
  static uint32_t w = 88675123;
  uint32_t t;
 
  t = x ^ (x << 11);
  x = y; y = z; z = w;
  return w = w ^ (w >> 19) ^ (t ^ (t >> 8));
}

This algorithm has a period of 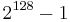2^{128}-1 and it passes the Diehard tests.

Notes

  1. ^ In C, the "^" caret represents the Bitwise XOR, and " << " the bit shift.

References

  1. ^ a b Marsaglia, George (July 2003). "Xorshift RNGs". Journal of Statistical Software Vol. 8 (Issue  14). http://www.jstatsoft.org/v08/i14/paper. 
  2. ^ Brent, Richard P. (August 2004). "Note on Marsaglia’s Xorshift Random Number Generators". Journal of Statistical Software Vol. 11 (Issue 5). http://www.jstatsoft.org/v11/i04/paper. 

External links

Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 7.1.2.A. 64-bit Xorshift Method", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, http://apps.nrbook.com/empanel/index.html#pg=345