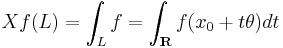X-ray transform

In mathematics, the X-ray transform (also called John transform) is an integral transform introduced by John (1938) that is one of the cornerstones of modern integral geometry. It is very closely related to the Radon transform, and coincides with it in two dimensions. In higher dimensions, the X-ray transform of a function is defined by integrating over lines rather than over hyperplanes as in the Radon transform. The X-ray transform derives its name from X-ray tomography because the X-ray transform of a function ƒ represents the scattering data of a tomographic scan through an inhomogeneous medium whose density is represented by the function ƒ. Inversion of the X-ray transform is therefore of practical importance because it allows one to reconstruct an unknown density ƒ from its known scattering data.

In detail, if ƒ is a compactly supported continuous function on the Euclidean space Rn, then the X-ray transform of ƒ is the function Xƒ defined on the set of all lines lines in Rn by

Xf(L) = \int_L f = \int_{\mathbf{R}} f(x_0%2Bt\theta)dt

where x0 is an initial point on the line and θ is a unit vector giving the direction of the line L. The latter integral is not regarded in the oriented sense: it is the integral with respect to the 1-dimensional Lebesgue measure on the Euclidean line L.

The X-ray transform satisfies an ultrahyperbolic wave equation called John's equation.

The Gauss hypergeometric function can be written as an X-ray transform (Gelfand, Gindikin & Graev 2003, 2.1.2).

References