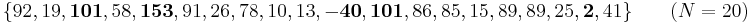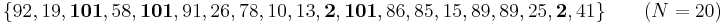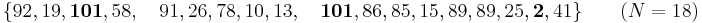Winsorising
Winsorising or Winsorization is the transformation of statistics by limiting extreme values in the statistical data to reduce the effect of possibly spurious outliers. It is named after the engineer-turned-biostatistician Charles P. Winsor (1895–1951). The effect is the same as clipping in signal processing.
The distribution of many statistics can be heavily influenced by outliers. A typical strategy is to set all outliers to a specified percentile of the data; for example, a 90% Winsorisation would see all data below the 5th percentile set to the 5th percentile, and data above the 95th percentile set to the 95th percentile. Winsorised estimators are usually more robust to outliers than their more standard forms, although there are alternatives, such as trimming, that will achieve a similar effect.
Example
Consider the data set consisting of:
The 5th percentile lies between -40 and 2, while the 95th percentile lies between 101 and 153. (Values shown in bold.) Then a 90% Winsorisation would result in the following:
Distinction from trimming
Note that Winsorizing is not equivalent to simply excluding data, which is a simpler procedure, called trimming.
In a trimmed estimator, the extreme values are discarded; in a Winsorized estimator, the extreme values are instead replaced by certain percentiles (the trimmed minimum and maximum).
Thus a Winsorized mean is not the same as a truncated mean. For instance, the 5% trimmed mean is the average of the 5th to 95th percentile of the data, while the 90% Winsorised mean sets the bottom 5% to the 5th percentile, the top 5% to the 95th percentile, and then averages the data. In the previous example the trimmed mean would be obtained from the smaller set:
More formally, they are distinct because the order statistics are not independent.
References
- Hasings, C., Mosteller, F., Tukey, J.W., Winsor, C.P. (1947) Low moments for small samples: a comparative study of order statistics, Annals of Mathematical Statistics, 18, 413–426.
- W. J. Dixon (1960). Simplified Estimation from Censored Normal Samples, The Annals of Mathematical Statistics, 31, 385–391.
- J. W. Tukey (1962) The Future of Data Analysis, The Annals of Mathematical Statistics, 33, p. 18