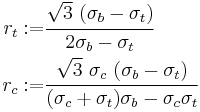Willam-Warnke yield criterion
The Willam-Warnke yield criterion [1] is a function that is used to predict when failure will occur in concrete and other cohesive-frictional materials such as rock, soil, and ceramics. This yield criterion has the functional form
where 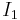 is the first invariant of the Cauchy stress tensor, and
is the first invariant of the Cauchy stress tensor, and  are the second and third invariants of the deviatoric part of the Cauchy stress tensor. There are three material parameters (
are the second and third invariants of the deviatoric part of the Cauchy stress tensor. There are three material parameters (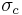 - the uniaxial compressive strength,
- the uniaxial compressive strength, 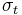 - the uniaxial tensile strength,
- the uniaxial tensile strength, 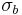 - the equibiaxial compressive strength) that have to be determined before the Willam-Warnke yield criterion may be applied to predict failure.
- the equibiaxial compressive strength) that have to be determined before the Willam-Warnke yield criterion may be applied to predict failure.
In terms of 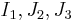 , the Willam-Warnke yield criterion can be expressed as
, the Willam-Warnke yield criterion can be expressed as
where  is a function that depends on
is a function that depends on 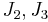 and the three material parameters and
and the three material parameters and  depends only on the material parameters. The function
depends only on the material parameters. The function  can be interpreted as the friction angle which depends on the Lode angle (
can be interpreted as the friction angle which depends on the Lode angle ( ). The quantity
). The quantity  is interpreted as a cohesion pressure. The Willam-Warnke yield criterion may therefore be viewed as a combination of the Mohr-Coulomb and the Drucker-Prager yield criteria.
is interpreted as a cohesion pressure. The Willam-Warnke yield criterion may therefore be viewed as a combination of the Mohr-Coulomb and the Drucker-Prager yield criteria.
Contents |
Willam-Warnke yield function
In the original paper, the three-parameter Willam-Warnke yield function was expressed as
where 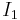 is the first invariant of the stress tensor,
is the first invariant of the stress tensor, 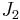 is the second invariant of the deviatoric part of the stress tensor,
is the second invariant of the deviatoric part of the stress tensor, 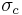 is the yield stress in uniaxial compression, and
is the yield stress in uniaxial compression, and  is the Lode angle given by
is the Lode angle given by
The locus of the boundary of the stress surface in the deviatoric stress plane is expressed in polar coordinates by the quantity 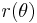 which is given by
which is given by
where
The quantities 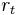 and
and 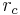 describe the position vectors at the locations
describe the position vectors at the locations 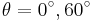 and can be expressed in terms of
and can be expressed in terms of 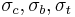 as
as
The parameter 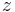 in the model is given by
in the model is given by
The Haigh-Westergaard representation of the Willam-Warnke yield condition can be written as
where
Modified forms of the Willam-Warnke yield criterion
An alternative form of the Willam-Warnke yield criterion in Haigh-Westergaard coordinates is the Ulm-Coussy-Bazant form [2] :
where
and
The quantities 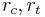 are interpreted as friction coefficients. For the yield surface to be convex, the Willam-Warnke yield criterion requires that
are interpreted as friction coefficients. For the yield surface to be convex, the Willam-Warnke yield criterion requires that 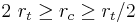 and
and 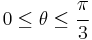 .
.
See also
References
- ^ Willam, K. J. and Warnke, E. P. (1975). Constitutive models for the triaxial behavior of concrete. Proceedings of the International Assoc. for Bridge and Structural Engineering , vol 19, pp. 1- 30.
- ^ Ulm, F-J., Coussy, O., Bazant, Z. (1999) The ‘‘Chunnel’’ Fire. I: Chemoplastic softening in rapidly heated concrete. ASCE Journal of Engineering Mechanics, vol. 125, no. 3, pp. 272-282.
- Chen, W. F. (1982). Plasticity in Reinforced Concrete. McGraw Hill. New York.
External links
- Kaspar Willam and E.P. Warnke (1974). Constitutive model for the triaxial behavior of concrete
- Palko, J. L. (1993). Interactive reliability model for whisker-toughened ceramics
- The ‘‘Chunnel’’ Fire. I: Chemoplastic softening in rapidly heated concrete by Franz-Josef Ulm, Olivier Coussy, and Zdeneˇk P. Bazˇant.
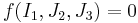
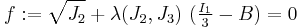
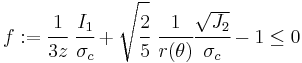
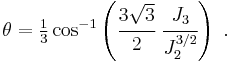
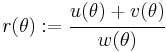
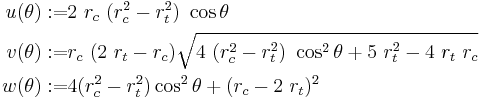
![r_c�:= \sqrt{\cfrac{6}{5}}\left[\cfrac{\sigma_b\sigma_t}{3\sigma_b\sigma_t %2B \sigma_c(\sigma_b - \sigma_t)}\right] ~;~~
r_t�:= \sqrt{\cfrac{6}{5}}\left[\cfrac{\sigma_b\sigma_t}{\sigma_c(2\sigma_b%2B\sigma_t)}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/cf6e230b9dec4524442afd5beb6f8492.png)
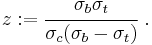
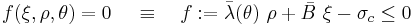
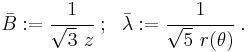
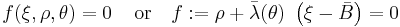
![\bar{\lambda}�:= \sqrt{\tfrac{2}{3}}~\cfrac{u(\theta)%2Bv(\theta)}{w(\theta)} ~;~~
\bar{B}�:= \tfrac{1}{\sqrt{3}}~\left[\cfrac{\sigma_b\sigma_t}{\sigma_b-\sigma_t}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/1bb6219aa43af44e008599cdb53508da.png)