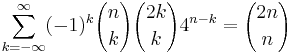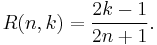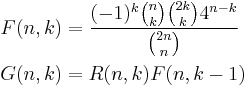Wilf–Zeilberger pair
In mathematics, specifically combinatorics, a Wilf–Zeilberger pair, or WZ pair, is a pair of functions that can be used to certify certain combinatorial identities. In particular, WZ pairs are instrumental in the evaluation of many sums involving binomial coefficients, factorials, and in general any hypergeometric series. A function's WZ counterpart may be used to find an equivalent, and much simpler sum. Although finding WZ pairs by hand is impractical in most cases, Gosper's algorithm provides a sure method to find a function's WZ counterpart, and can be implemented in a symbolic manipulation program.
Contents |
Definition
Two functions, F and G, form a pair if and only if the following two conditions hold:
Together, these conditions ensure that the sum
because the function G telescopes:
Example
A Wilf–Zeilberger pair can be used to verify the identity
using the proof certificate
Define the following functions:
Now F and G will form a Wilf-Zeilberger pair:
See also
References
- Marko Petkovsek, Herbert Wilf and Doron Zeilberger (1996). A=B. AK Peters. ISBN 1568810636. http://www.math.upenn.edu/~wilf/AeqB.html.
- Tefera, Akalu (2010), "What Is . . . a Wilf-Zeilberger Pair?", AMS Notices 57 (04): 508–509, http://www.ams.org/notices/201004/rtx100400508p.pdf.
External links
- Gosper's algorithm gives a method for generating WZ pairs when they exist.
- Generatingfunctionology provides details on the WZ method of identity certification.

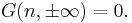
![\sum_{k=-\infty}^\infty [F(n%2B1,k)-F(n,k)] = 0](/2012-wikipedia_en_all_nopic_01_2012/I/162146a25c8b7fb9eb2efcca6010ee0d.png)
![\begin{align} \sum_{k=-\infty}^\infty [F(n%2B1,k)-F(n,k)]
& {} = \lim_{M \to \infty} \sum_{k=-M}^M[F(n%2B1,k)-F(n,k)] \\
& {} = \lim_{M \to \infty} \sum_{k=-M}^M [G(n,k%2B1)-G(n,k)] \\
& {} = \lim_{M \to \infty} [G(n,M%2B1)-G(n,-M)] \\
& {} = 0-0 \\
& {} = 0.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/d9122a071024895d12f93f813e445bd9.png)