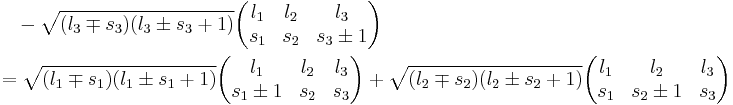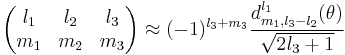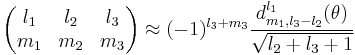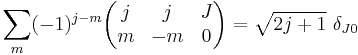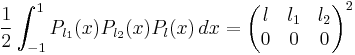Wigner 3-j symbols
In quantum mechanics, the Wigner 3-j symbols, also called 3j or 3-jm symbols, are related to Clebsch–Gordan coefficients through
Inverse relation
The inverse relation can be found by noting that j1 - j2 - m3 is an integer number and making the substitution 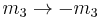
Symmetry properties
The symmetry properties of 3j symbols are more convenient than those of Clebsch–Gordan coefficients. A 3j symbol is invariant under an even permutation of its columns:
An odd permutation of the columns gives a phase factor:
Changing the sign of the 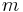 quantum numbers also gives a phase:
quantum numbers also gives a phase:
Regge symmetries also give
Selection rules
The Wigner 3j is zero unless all these conditions are satisfied:
Scalar invariant
The contraction of the product of three rotational states with a 3j symbol,
is invariant under rotations.
Orthogonality relations
Relation to spherical harmonics
The 3jm symbols give the integral of the products of three spherical harmonics
with 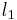 ,
, 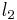 and
and 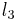 integers.
integers.
Relation to integrals of spin-weighted spherical harmonics
Recursion relations
Asymptotic expressions
For 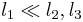 a non-zero 3-j symbol has
a non-zero 3-j symbol has
where 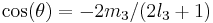 and
and 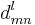 is a Wigner function. Generally a better approximation obeying the Regge symmetry is given by
is a Wigner function. Generally a better approximation obeying the Regge symmetry is given by
where 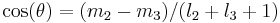 .
.
Other properties
See also
References
- L. C. Biedenharn and J. D. Louck, Angular Momentum in Quantum Physics, volume 8 of Encyclopedia of Mathematics, Addison-Wesley, Reading, 1981.
- D. M. Brink and G. R. Satchler, Angular Momentum, 3rd edition, Clarendon, Oxford, 1993.
- A. R. Edmonds, Angular Momentum in Quantum Mechanics, 2nd edition, Princeton University Press, Princeton, 1960.
- Maximon, Leonard C. (2010), "3j,6j,9j Symbols", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248, http://dlmf.nist.gov/34
- Varshalovich, D. A.; Moskalev, A. N.; Khersonskii, V. K. (1988). Quantum Theory of Angular Momentum. World Scientific Publishing Co..
- E. P. Wigner, "On the Matrices Which Reduce the Kronecker Products of Representations of Simply Reducible Groups", unpublished (1940). Reprinted in: L. C. Biedenharn and H. van Dam, Quantum Theory of Angular Momentum, Academic Press, New York (1965).
- Moshinsky, Marcos (1962). "Wigner coefficients for the SU3 group and some applications". Rev. Mod. Phys. 34 (4): 813. Bibcode 1962RvMP...34..813M. doi:10.1103/RevModPhys.34.813.
- Baird, G. E.; Biedenharn, L. C. (1963). "On the representation of the semisimple Lie Groups. II.". J. Math. Phys. 4: 1449. Bibcode 1963JMP.....4.1449B. doi:10.1063/1.1703926.
- Swart de, J. J. (1963). "The octet model and its Glebsch-Gordan coefficients". Rev. Mod. Phys. 35 (4): 916. Bibcode 1963RvMP...35..916D. doi:10.1103/RevModPhys.35.916.
- Baird, G. E.; Biedenharn, L. C. (1964). "On the representations of the semisimple Lie Groups. III. The explicit conjugation Operation for SUn". J. Math. Phys. 5: 1723. Bibcode 1964JMP.....5.1723B. doi:10.1063/1.1704095.
- Horie, Hisashi (1964). "Representations of the symmetric group and the fractional parentage coefficients". J. Phys. Soc. Jpn. 19: 1783. doi:10.1143/JPSJ.19.1783.
- P. McNamee, S. J.; Chilton, Frank (1964). "Tables of Clebsch-Gordan coefficients of SU3". Rev. Mod. Phys. 36 (4): 1005. Bibcode 1964RvMP...36.1005M. doi:10.1103/RevModPhys.36.1005.
- Hecht, K. T. (1965). "SU3 recoupling and fractional parentage in the 2s-1d shell". Nucl. Phys. 62 (1): 1. Bibcode 1965NucPh..62....1H. doi:10.1016/0029-5582(65)90068-4.
- Itzykson, C.; Nauenberg, M. (1966). "Unitary groups: representations and decompositions". Rev. Mod. Phys. 38 (1): 95. Bibcode 1966RvMp...38...95I. doi:10.1103/RevModPhys.38.95.
- Kramer, P. (1967). "Orbital fractional parentage coefficients for the harmonic oscillator shell model". Z. Physik 205 (2): 181. Bibcode 1967ZPhy..205..181K. doi:10.1007/BF01333370.
- Kramer, P. (1968). "Recoupling coefficients of the symmetric group for shell and cluster model configurations". Z. Physik 216 (1): 68. Bibcode 1968ZPhy..216...68K. doi:10.1007/BF01380094.
- Hecht, K. T.; Pang, Sing Ching (1969). "On the Wigner Supermultiplet Scheme". J. Math. Phys. 10 (9): 1571. Bibcode 1969JMP....10.1571H. doi:10.1063/1.1665007.
- Lezuo, K. J. (1972). "The symmetric group and the Gel'fand basis of U(3). Generalizations of the Dirac identity". J. Math. Phys. 13 (9): 1389. Bibcode 1972JMP....13.1389L. doi:10.1063/1.1666151.
- Draayer, J. P.; Akiyama, Yoshimi (1973). "Wigner and Racah coefficients for SU3". J. Math. Phys. 14 (12): 1904. Bibcode 1973JMP....14.1904D. doi:10.1063/1.1666267.
- Akiyama, Yoshimi; Draayer, J. P. (1973). "A users' guide to fortran programs for Wigner and Racah coefficients of SU3". Comp. Phys. Comm. 5: 405. Bibcode 1973CoPhC...5..405A. doi:10.1016/0010-4655(73)90077-5.
- Paldus, Josef (1974). "Group theoretical approach to the configuration interaction and perturbation theory calculations for atomic and molecular systems". J. Chem. Phys 61 (12): 5321. Bibcode 1974JChPh..61.5321P. doi:10.1063/1.1681883.
- Schulten, Klaus; Gordon, Roy G. (1975). "Exact recursive evaluation of 3j and 6j-coefficients for quantum mechanical coupling of angular momenta". J. Math. Phys. 16 (10): 1961–1970. Bibcode 1975JMP....16.1961S. doi:10.1063/1.522426.
- Haacke, E. M.; Moffat, J. W.; Savaria, P. (1976). "A calculation of SU(4) Glebsch-Gordan coefficients". J. Math. Phys. 17 (11): 2041. Bibcode 1976JMP....17.2041H. doi:10.1063/1.522843.
- Paldus, Josef (1976). "Unitary-group approach to the many-electron correlation problem: Relation of Gelfand and Weyl tableau formulations". Phys. Rev. A. 14 (5): 1620. Bibcode 1976PhRvA..14.1620P. doi:10.1103/PhysRevA.14.1620.
- Bickerstaff, R. P.; Butler, P. H.; Butts, M. B.; Haase, R. w.; Reid, M. F. (1982). "3jm and 6j tables for some bases of SU6 and SU3". J. Phys. A 15: 1087. Bibcode 1982JPhA...15.1087B. doi:10.1088/0305-4470/15/4/014.
- Sarma, C. R.; Sahasrabudhe, G. G. (1980). "Permutational symmetry of many particle states". J. Math. Phys. 21 (4): 638. Bibcode 1980JMP....21..638S. doi:10.1063/1.524509.
- Chen, Jin-Quan; Gao, Mei-Juan (1982). "A new approach to permutation group representation". J. Math. Phys. 23: 928. Bibcode 1982JMP....23..928C. doi:10.1063/1.525460.
- Sarma, C. R. (1982). "Determination of basis for the irreducible representations of the unitary group for U(p+q)↓U(p)×U(q)". J. Math. Phys. 23 (7): 1235. Bibcode 1982JMP....23.1235S. doi:10.1063/1.525507.
- Chen, J.-Q.; Chen, X.-G. (1983). "The Gel'fand basis and matrix elements of the graded unitary group U(m/n)". J. Phys. A 16 (15): 3435. Bibcode 1983JPhA...16.3435C. doi:10.1088/0305-4470/16/15/010.
- Nikam, R. S.; Dinesha, K. V.; Sarma, C. R. (1983). "Reduction of inner-product representations of unitary groups". J. Math. Phys. 24 (2): 233. Bibcode 1983JMP....24..233N. doi:10.1063/1.525698.
- Chen, Jin-Quan; Collinson, David F.; Gao, Mei-Juan (1983). "Transformation coefficients of permutation groups". J. Math. Phys. 24: 2695. Bibcode 1983JMP....24.2695C. doi:10.1063/1.525668.
- Chen, Jin-Quan; Gao, Mei-Juan; Chen, Xuan-Gen (1984). "The Clebsch-Gordan coefficient for SU(m/n) Gel'fand basis". J. Phys. A 17 (3): 481. Bibcode 1984JPhA...17..727K. doi:10.1088/0305-4470/17/3/011.
- Wei, Liqiang (1999). "Unified approach for exact calculation of angular momentum coupling and recoupling coefficients". Comp. Phys. Comm. 120 (2–3): 222–230. Bibcode 1999CoPhC.120..222W. doi:10.1016/S0010-4655(99)00232-5.
External links
- Stone, Anthony. "Wigner coefficient calculator". http://www-stone.ch.cam.ac.uk/wigner.shtml. (Gives exact answer)
- Volya, A.. "Clebsch-Gordan, 3-j and 6-j Coefficient Web Calculator". http://www.volya.net/vc/vc.php. (Numerical)
- Stevenson, Paul. Clebsch-O-Matic. Bibcode 2002CoPhC.147..853S. doi:10.1016/S0010-4655(02)00462-9. http://personal.ph.surrey.ac.uk/~phs3ps/cleb.html.
- 369j-symbol calculator at the Plasma Laboratory of Weizmann Institute of Science (Numerical)
- Frederik J Simons: Matlab software archive, the code THREEJ.M
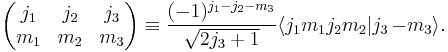
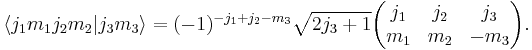
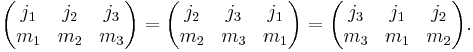
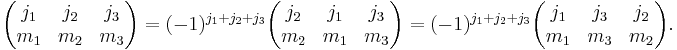
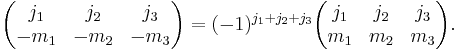
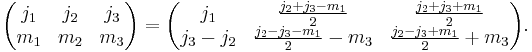
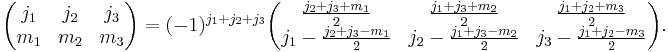
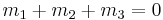
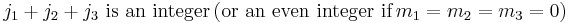
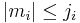
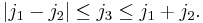
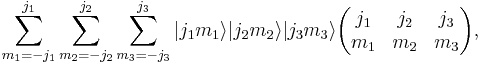
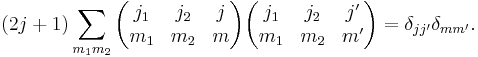
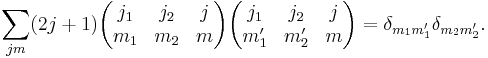
![\begin{align}
& {} \quad \int Y_{l_1m_1}(\theta,\varphi)Y_{l_2m_2}(\theta,\varphi)Y_{l_3m_3}(\theta,\varphi)\,\sin\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi \\
& =
\sqrt{\frac{(2l_1%2B1)(2l_2%2B1)(2l_3%2B1)}{4\pi}}
\begin{pmatrix}
l_1 & l_2 & l_3 \\[8pt]
0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
l_1 & l_2 & l_3\\
m_1 & m_2 & m_3
\end{pmatrix}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/3d701a69eb30c470385a582e40b73b5c.png)
![\begin{align}
& {} \quad \int d{\mathbf{\hat n}} {}_{s_1} Y_{j_1 m_1}({\mathbf{\hat n}})
{}_{s_2} Y_{j_2m_2}({\mathbf{\hat n}}) {}_{s_3} Y_{j_3m_3}({\mathbf{\hat
n}}) \\[8pt]
& = \sqrt{\frac{(2j_1%2B1)(2j_2%2B1)(2j_3%2B1)}{4\pi}}
\begin{pmatrix}
j_1 & j_2 & j_3\\
m_1 & m_2 & m_3
\end{pmatrix}
\begin{pmatrix}
j_1 & j_2 & j_3\\
-s_1 & -s_2 & -s_3
\end{pmatrix}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/8803c8280f2ee3e7af477cac6ff1808c.png)