Whitehead's lemma
Whitehead's lemma is a technical result in abstract algebra used in algebraic K-theory. It states that a matrix of the form
is equivalent to the identity matrix by elementary transformations (that is, transvections):
Here, 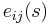 indicates a matrix whose diagonal block is
indicates a matrix whose diagonal block is 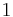 and
and 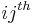 entry is
entry is  .
.
The name "Whitehead's lemma" also refers to the closely related result[1] that the derived group of the stable general linear group is the group generated by elementary matrices. In symbols,
![\operatorname{E}(A) = [\operatorname{GL}(A),\operatorname{GL}(A)]](/2012-wikipedia_en_all_nopic_01_2012/I/fa65e30f09e43aeea20f4043115c57ea.png) .
.
This holds for the stable group (the direct limit of matrices of finite size) over any ring, but not in general for the unstable groups, even over a field. For instance for
one has:
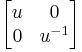
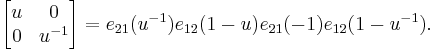
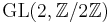
![\operatorname{Alt}(3) \cong [\operatorname{GL}_2(\mathbb{Z}/2\mathbb{Z}),\operatorname{GL}_2(\mathbb{Z}/2\mathbb{Z})] < \operatorname{E}_2(\mathbb{Z}/2\mathbb{Z}) = \operatorname{SL}_2(\mathbb{Z}/2\mathbb{Z}) = \operatorname{GL}_2(\mathbb{Z}/2\mathbb{Z}) \cong \operatorname{Sym}(3).](/2012-wikipedia_en_all_nopic_01_2012/I/e5140de9aab38f5b9633c5f688108210.png)